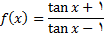مشتق / مشتق توابع مثلثاتی
برای اینکه نشان دهیم تابع سینوسی دارای مشتق است, از فرمولی که به صورت زیر است استفاده میکنیم و قضایا را بکار میگیریم.
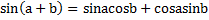
فرض کنید تابع
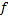 به صورت زیر تعریف شده باشد
به صورت زیر تعریف شده باشد
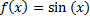
از تعریف مشتق داریم
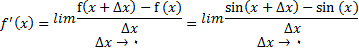
با استفاده از فرمول (1) برای
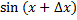 خواهیم داشت:
خواهیم داشت:
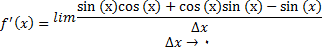
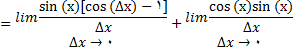
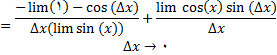
با توجه به معادلات زیر
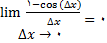 (3)
(3)
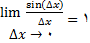 (4)
(4)
معادلات (3) و (4) را در معادله (2) جانشین میکنیم و به دست میاوریم
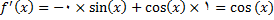
که در واقع قضیه زیر را اثبات کرده ایم
قضیه 1:
(5) 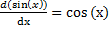
مثال 1: تابع
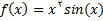 داده شده است
داده شده است
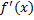 را بیابید.
را بیابید.
حل: با استفاده از قضیه مشتق حاصلضرب دو تابع را می یابیم.
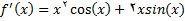
برای پیدا کردن مشتق تابع کسینوسی مانند مشتق تابع سینوسی عمل میکنیم. فرض کنید
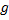 به صورت زیر تعریف شده است
به صورت زیر تعریف شده است
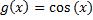
در اینصورت
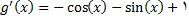 بنابراین قضیه زیر را خواهم داشت
بنابراین قضیه زیر را خواهم داشت
قضیه 2: 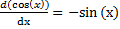
مثال 2: تابع 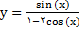 داده شده است,
داده شده است,
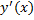 را پیدا کنید.
را پیدا کنید.
حل: با استفاده از قضیه داریم
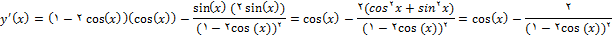
چون
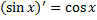 و
و
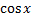 برای تمام مقادیر
برای تمام مقادیر
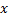 تعریف شده است, پس تابع سینوسی همه جا مشتق پذیر و در نتیجه همه جا پیوسته است. به طور مشابه, تابع کسینوسی نیز همه جا مشتق پذیر و پیوسته است. چون بیشترین مقداری که هر یک از دو تابع میتواند داشته باشد 1 و کمترین مقدارشان 1- است با توجه به قضیه مقدار میانی برد هریک از دو تابع
تعریف شده است, پس تابع سینوسی همه جا مشتق پذیر و در نتیجه همه جا پیوسته است. به طور مشابه, تابع کسینوسی نیز همه جا مشتق پذیر و پیوسته است. چون بیشترین مقداری که هر یک از دو تابع میتواند داشته باشد 1 و کمترین مقدارشان 1- است با توجه به قضیه مقدار میانی برد هریک از دو تابع
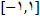 است.
است.
اکنون در مورد نمودار تابع سینوسی بحث میکنیم. فرض کنید
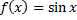 در اینصورت
در اینصورت
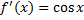 برای تعین نقاطی که در آن نقاط , نمودار مماس افقی دارد, بایستی قرار دهیم
برای تعین نقاطی که در آن نقاط , نمودار مماس افقی دارد, بایستی قرار دهیم
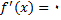 , و به دست میآید
, و به دست میآید
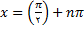 که در ان
که در ان
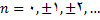 به ازای این مقادیر,
به ازای این مقادیر,
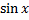 یا
یا
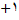 و یا
و یا
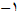 است, و این دو مقدار بزرگترین و کوچکترین مقادیری هستند که سینوس به خود میگیرد. نمودار, محور
است, و این دو مقدار بزرگترین و کوچکترین مقادیری هستند که سینوس به خود میگیرد. نمودار, محور
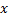 را در نقاطی که
را در نقاطی که
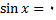 ,یعنی نقاطی که
,یعنی نقاطی که
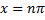 , قطع میکند که
, قطع میکند که
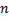 عددی صحیح و دلخواه است. با این اطلاعات, نمودار تابع سینوسی در شکل زیر رسم شده است.
عددی صحیح و دلخواه است. با این اطلاعات, نمودار تابع سینوسی در شکل زیر رسم شده است.
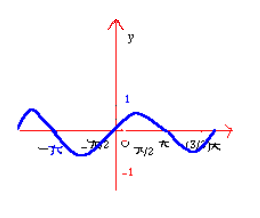
برای رسم نمودار تابع کسینوسی, از اتحاد زیر استفاده میکنیم
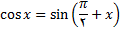
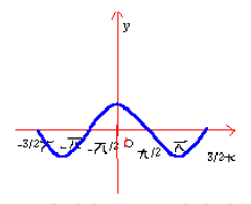
بنابراین نمودار تابع کسینوسی را می توان از نمودار تابع سینوسی با انتقال محور
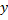 به اندازه
به اندازه
 به طرف راست در آورد.
به طرف راست در آورد.
در تمرین های زیر, مشتق توابع داده شده را به دست آورید.
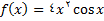
2.
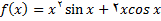
3.
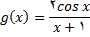
4.
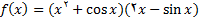
5.

6.