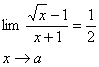مفاهیم اولیه حد
تعريف 1 : فرض كنيد
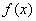 تابعي باشد كه در تمام
نقاط يك بازه باز مانند
تابعي باشد كه در تمام
نقاط يك بازه باز مانند
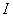 كه شامل عدد
كه شامل عدد
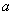 ، بجز احتمالا
درخود
، بجز احتمالا
درخود
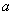 تعريف بشود .
حد
تعريف بشود .
حد
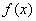 وقتي
وقتي
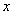 به سمت
به سمت
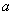 ميل ميكند برابر
ميل ميكند برابر
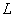 است و مي نويسيم :
است و مي نويسيم :
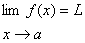
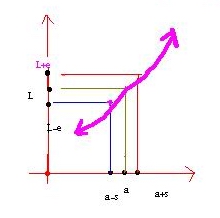
اگر به ازاي هر
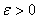 هرقدر كوچك ،عدد مثبتي چون
هرقدر كوچك ،عدد مثبتي چون
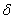 وجود داشته باشد كه :
وجود داشته باشد كه :
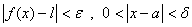
تعريف 2 : حاكي است كه وقتي
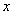 به سمت عددي مانند
به سمت عددي مانند
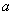 ميل كند مقادير
ميل كند مقادير
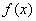 به سمت حدي چون
به سمت حدي چون
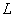 ميل ميكند اگر با
انتخاب
ميل ميكند اگر با
انتخاب
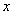 به اندازه كافي نزديك
به
به اندازه كافي نزديك
به
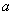 ، با شرط
، با شرط
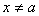 بتوان قدر مطلق اختلاف
بين
بتوان قدر مطلق اختلاف
بين
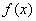 و
و
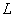 را به قدر دلخواه كوچك
كرد .
را به قدر دلخواه كوچك
كرد .
توجه به اين نكته مهم است كه در تعريف فوق از مقدار تابع
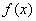 براي
براي
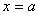 چيزي گفته نشده است
يعني براي وجود
چيزي گفته نشده است
يعني براي وجود
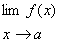 حتي لازم نيست كه تابع براي
حتي لازم نيست كه تابع براي
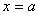 تعريف بشود .
تعريف بشود .
يك تعبير هندسي تعريف تعریف حد تابع , براي تابعي چون
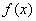 در شكل فوق نمايش داده
شده است .
تنها بخشي از نمودار تابع كه نزديك نقطه به طول
در شكل فوق نمايش داده
شده است .
تنها بخشي از نمودار تابع كه نزديك نقطه به طول
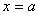 است درشكل نشان داده
شده است چون
است درشكل نشان داده
شده است چون
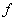 لزوما در
لزوما در
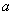 تعريف نمي شود نقطه اي
بطول
تعريف نمي شود نقطه اي
بطول
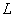 روي نمودار وجود ندارد.
مشاهده كنيد كه وقتي
روي نمودار وجود ندارد.
مشاهده كنيد كه وقتي
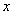 روي محور افقي بين
روي محور افقي بين
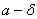 و
و
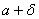 قرار داشته باشد ،
قرار داشته باشد ،
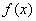 روي محور قائم بين
روي محور قائم بين
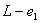 و
و
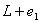 واقع مي شود . بعبارت ديگر
، با محدود كردن
واقع مي شود . بعبارت ديگر
، با محدود كردن
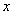 روي محور افقي بين
روي محور افقي بين
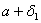 و
و
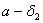 ميتوان
ميتوان
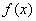 را روي محور قائم
بين
را روي محور قائم
بين
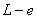 ,
,
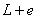 محدود كرد بنابراين :
محدود كرد بنابراين :
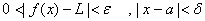
مثال 1
فرض كنيد تابع
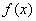 به معادله
به معادله
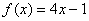 تعريف شده باشد . اگر
تعريف شده باشد . اگر
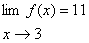
مقدار
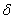 را براي
را براي
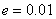 پيداكنيد بطوري كه
پيداكنيد بطوري كه
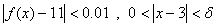
حل :

با فرض
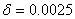 داريم :
داريم :
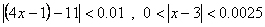
در اين مثال بعنوان
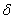 مورد نظر ، مي توانيم
بجاي
مورد نظر ، مي توانيم
بجاي
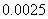 هر عدد مثبت كوچكتر از
هر عدد مثبت كوچكتر از
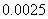 را هم انتخاب كنيم يعني
اگر
را هم انتخاب كنيم يعني
اگر
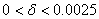 و عبارت
و عبارت
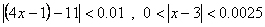 برقرار باشد ، آنگاه وقتي كه
برقرار باشد ، آنگاه وقتي كه
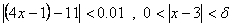 زيرا اگر
زيرا اگر
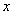 درنامساوي
درنامساوي
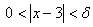 صدق كند ، آنگاه در
نامساوي
صدق كند ، آنگاه در
نامساوي
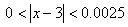 نيز صدق ميكند .
نيز صدق ميكند .
مثال 2 :
با استفاده از تعريف 1 ثابت كنيد كه
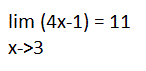
حل :
نخستين شرط تعريف اين است كه به
ازاي هر عدد متعلق به يك بازه باز كه شامل
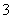 باشد
، بجز احتمالا
باشد
، بجز احتمالا
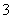 ,
,
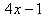 معين باشد چون
معين باشد چون
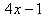 به ازاي همه مقادير
به ازاي همه مقادير
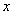 معين است ، هر بازه باز
شامل
معين است ، هر بازه باز
شامل
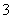 اين شرط را برآورده
ميكند .
حال بايد نشان دهيم كه به ازاي هر
اين شرط را برآورده
ميكند .
حال بايد نشان دهيم كه به ازاي هر
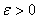 يك
يك
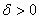 كه وقتي
كه وقتي
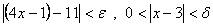
ازمثال 1 مي بينيم كه
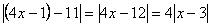 بنابراين مي خواهيم وقتي كه
بنابراين مي خواهيم وقتي كه
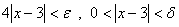 يا
وقتي كه
يا
وقتي كه
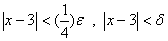 لذا
اگر فرض كنيم
لذا
اگر فرض كنيم
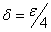 داريم
داريم
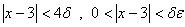 به
عبارت ديگر ، وقتي كه
به
عبارت ديگر ، وقتي كه
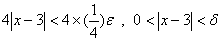 وقتي كه
وقتي كه
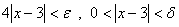 كه از
آن نتيجه ميشود
كه از
آن نتيجه ميشود
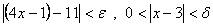 با اين
شرط كه
با اين
شرط كه
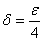 و اين ثابت ميكند كه
و اين ثابت ميكند كه
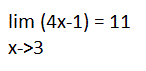
مثال 3
: با استفاده از تعريف حد ثابت كنيد كه
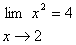
حل :
چون به ازاي هر مقدار از
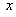 ،
،
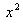 معين است ، هر بازه باز
شامل 2 نخستين شرط تعريف 1 – 4 را برآورده ميكند .
بايد
نشان دهيم كه براي هر
معين است ، هر بازه باز
شامل 2 نخستين شرط تعريف 1 – 4 را برآورده ميكند .
بايد
نشان دهيم كه براي هر
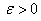 يك
يك
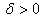 وجود دارد كه
وجود دارد كه
(6)
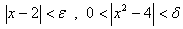
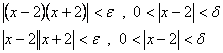
(7)
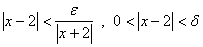
چون ميخواهيم به ازاي تمام مقادير
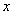 در بازه
در بازه
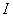 مورد نياز در تعريف 1 – 4 ، داشته باشيم
مورد نياز در تعريف 1 – 4 ، داشته باشيم
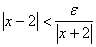 يك بازه باز خاص براي
يك بازه باز خاص براي
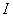 اختيار ميكنيم و با كمك آن يك كران پائين براي
اختيار ميكنيم و با كمك آن يك كران پائين براي
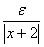 به دست ميآوريم . اگر
به دست ميآوريم . اگر
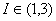 باشد كه مركزش 2 و شعاعش 1 است ، آنگاه به ازاي
هر
باشد كه مركزش 2 و شعاعش 1 است ، آنگاه به ازاي
هر
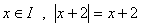 بعلاوه به ازاي هر
بعلاوه به ازاي هر
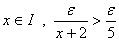 پس به ازاي مقادير
پس به ازاي مقادير
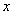 در
در
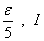 كران پائيني براي
كران پائيني براي
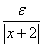 است ، در نتيجه از اين كران پائين
شعاع بازه
است ، در نتيجه از اين كران پائين
شعاع بازه
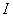 ، كوچكترين را بعنوان
، كوچكترين را بعنوان
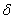 اختيار ميكنيم
يعني
اختيار ميكنيم
يعني
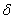 را كوچكترين
را كوچكترين
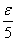 و 1 درنظر ميگيريم و مي نويسيم
و 1 درنظر ميگيريم و مي نويسيم
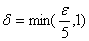 پس
پس
(8)
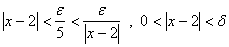
به شرطي كه
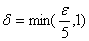
، از عبارت (8) نتيجه مي شودكه به ازاي اين
مقدار از
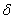 ،عبارت (7) و عبارت معادل آن (6) برقرارند . براي اينكه اهميت
،عبارت (7) و عبارت معادل آن (6) برقرارند . براي اينكه اهميت
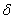 را نشان دهيم چند مقدارممكن براي
را نشان دهيم چند مقدارممكن براي
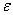 را در نظر ميگيريم
. اگر
را در نظر ميگيريم
. اگر
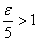 يعني اگر
يعني اگر
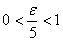 يعني
يعني
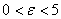 مي نويسيم
مي نويسيم
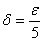 .
آنگاه وقتي كه
.
آنگاه وقتي كه
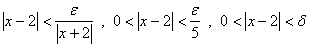 پس به ازاي هر
پس به ازاي هر
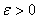 وقتي كه
وقتي كه
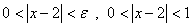 و
و
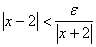 عبارت
عبارت
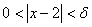 ايجاب ميكند كه
ايجاب ميكند كه
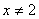 و
و
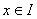 .
.
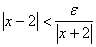 معادل است با عبارت
معادل است با عبارت
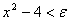
بنابراين تعريف 1 – 4
برقرار است
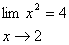 .
.
قضيه زير نشان مي دهدكه يك تابع نمي تواند در يك زمان به سمت دو حد مختلف
ميل كند . اين قضيه را قضيه يكتائي مي ناميم زيرا تضمين ميكندكه اگر يك تابع حد
داشته باشد ، آن حد يكتااست .
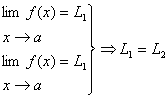
تمرين :
در تمرينهاي زير
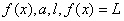 داده شده اند وبراي
داده شده اند وبراي
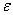 مفروض ز ماني كه
مفروض ز ماني كه
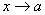 عددي مانند
عددي مانند
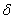 وجود دارد به شرطي كه
وجود دارد به شرطي كه
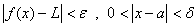
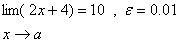
2.
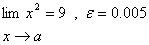
3.
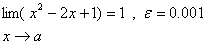
4.
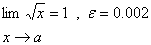
5.
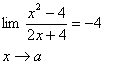
در تمرينات زير با استفاده از تعريف
حد به ازاي هر
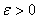 يك
يك
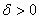 پيدا كنيد كه داشته باشيم
پيدا كنيد كه داشته باشيم
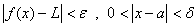
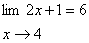
7.
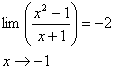
8.
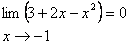
9.
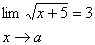
10.