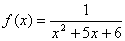ریاضی عمومی / حد بینهایت
فرض كنيد تابع f بصورت زير تعريف شده باشد
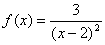
نمودار اين تابع در شكل
زير رسم شده است .
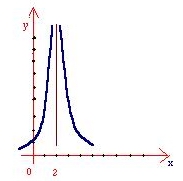
براي
اينكه نشان دهيم وقتي
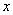 با مقادير بزرگتر از 2
به 2 نزديك مي شود
،
با مقادير بزرگتر از 2
به 2 نزديك مي شود
،
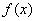 به طور بيكران افزايش مي
يابد پس می نویسیم
به طور بيكران افزايش مي
يابد پس می نویسیم
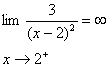
حال
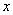 را از سمت چپ به 2 ميل ميدهيم و بررسي
ميكنيم كه وقتي
را از سمت چپ به 2 ميل ميدهيم و بررسي
ميكنيم كه وقتي
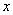 با مقادير کمتر
از 2 به 2 نزديك و نزدیکتر مي شود
،
با مقادير کمتر
از 2 به 2 نزديك و نزدیکتر مي شود
،
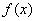 به طور بيكران افزايش مي يابد پس
به طور بيكران افزايش مي يابد پس
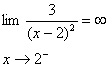
بنابراين وقتي
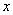 از سمت راست يا از سمت چپ به 2 نزديك
ميشود
از سمت راست يا از سمت چپ به 2 نزديك
ميشود
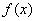 بطور بيكران افزايش مييابد و لذا
مينويسيم :
بطور بيكران افزايش مييابد و لذا
مينويسيم :
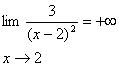
تعريف 1
فرض كنيد تابع
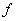 به ازاي هر عدد واقع دريك بازه باز
چون
به ازاي هر عدد واقع دريك بازه باز
چون
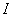 كه
شامل عددي مانند
كه
شامل عددي مانند
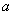 است بجز احتمالا در خود عدد
است بجز احتمالا در خود عدد
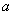 تعريف شده باشد .
وقتي
تعريف شده باشد .
وقتي
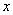 به سمت
به سمت
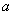 ميل كند ،
ميل كند ،
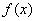 به طور بيكران افزايش مي يابد و
مينويسيم :
به طور بيكران افزايش مي يابد و
مينويسيم :
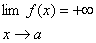
هرگاه براي هر
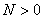 ، يك
، يك
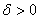 وجود داشته باشد كه وقتي ،
وجود داشته باشد كه وقتي ،
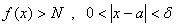 راه ديگر بيان تعريف فوق به شرح زير است
راه ديگر بيان تعريف فوق به شرح زير است
وقتي
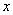 به سمت عددي چون
به سمت عددي چون
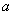 ميل ميكند
ميل ميكند
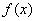 به طور بيكران افزايش مي يابد ،
هرگاه به ازاي تمام
به طور بيكران افزايش مي يابد ،
هرگاه به ازاي تمام
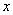 هائي كه به اندازه كافي نزديك به
هائي كه به اندازه كافي نزديك به
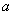 باشند و مساوي با
باشند و مساوي با
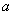 نباشند
، بتوانيم
نباشند
، بتوانيم
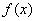 را به اندازه دلخواه بزرگ كنيم ( يعني
انرا از هر عدد مثبت بزرگتر سازيم ) .
را به اندازه دلخواه بزرگ كنيم ( يعني
انرا از هر عدد مثبت بزرگتر سازيم ) .
توجه : دوباره تاكيد ميكنيم,
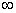 یک عدد حقيقي نيست .
بنابراين وقتي مينويسيم
یک عدد حقيقي نيست .
بنابراين وقتي مينويسيم
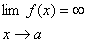 ، معني آن مثل
، معني آن مثل
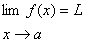 نيست كه در آن
نيست كه در آن
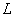 يك عدد حقيقي است.
يك عدد حقيقي است.
معادله (1) را مي توان
چنين خواند . حد
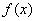 وقتي
وقتي
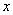 به سمت
به سمت
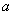 ميل ميكند بينهايت است . در اين مورد
حد وجود ندارد . اما نماد
ميل ميكند بينهايت است . در اين مورد
حد وجود ندارد . اما نماد
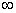 رفتار مقادير تابع را وقتي
رفتار مقادير تابع را وقتي
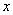 به
به
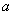 نزديك ميشود ، مشخص نمايد . به طريق مشابه ميتوانيم رفتار تابعي را كه
مقادير آن به طور بيكران افزايش مي يابد را مشخص كنيم .
براي اينكه به اين مطلب
هدايت شويم ، تابع
نزديك ميشود ، مشخص نمايد . به طريق مشابه ميتوانيم رفتار تابعي را كه
مقادير آن به طور بيكران افزايش مي يابد را مشخص كنيم .
براي اينكه به اين مطلب
هدايت شويم ، تابع
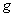 را كه بصورت زير تعريف ميشود در نظر
ميگيريم
را كه بصورت زير تعريف ميشود در نظر
ميگيريم
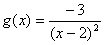
نمودار اين تابع در شكل زير رسم شده است .
مقادير تابع
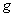 كه از
كه از
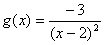 بدست مي ايند قرينه تابع
بدست مي ايند قرينه تابع
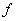 است كه از تابع
است كه از تابع
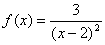 بدست ميايد . پس وقتي
بدست ميايد . پس وقتي
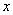 چه از سمت راست و چه از سمت چپ
به 2 ميل كند
چه از سمت راست و چه از سمت چپ
به 2 ميل كند
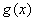 بطور بيكران كاهش ميابد بنابراين
مينويسيم :
بطور بيكران كاهش ميابد بنابراين
مينويسيم :
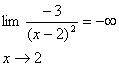
تعريف 2: تابع
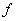 به ازاي هر عدد واقع در بازه بازي
مانند
به ازاي هر عدد واقع در بازه بازي
مانند
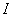 كه شامل
كه شامل
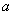 مي باشد بجز احتمالا در خود
مي باشد بجز احتمالا در خود
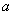 تعريف شده باشد . وقتي
تعريف شده باشد . وقتي
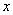 به سمت
به سمت
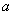 ميل كند
ميل كند
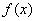 بطور بيكران كاهش مي يابد و مي
نويسيم :
بطور بيكران كاهش مي يابد و مي
نويسيم :
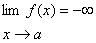
هرگاه براي هرعدد
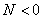 يك
يك
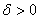 وجود داشته باشد كه وقتي
وجود داشته باشد كه وقتي
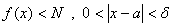
توجه : معادله (2) را ميتوان
چنين خواند ، حد
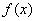 را وقتي
را وقتي
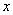 به سمت
به سمت
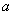 ميل مي كند بينهايت منفي است . بازهم
مشاهده ميكنيد كه حد وجود ندارد و نماد
ميل مي كند بينهايت منفي است . بازهم
مشاهده ميكنيد كه حد وجود ندارد و نماد
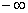 رفتار تابع را وقتي
رفتار تابع را وقتي
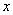 به
به
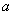 نزديك مي شود نشان مي دهد . مي توان
حد هاي يكطرفه اي را كه بينهايت باشد نيز درنظر بگيريم به ويژه داريم
نزديك مي شود نشان مي دهد . مي توان
حد هاي يكطرفه اي را كه بينهايت باشد نيز درنظر بگيريم به ويژه داريم
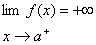
اگر
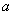 براي تمام اعداد در بازه بازي چون
براي تمام اعداد در بازه بازي چون
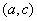 تعريف شده باشد و اگر
براي هر
تعريف شده باشد و اگر
براي هر
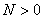 يك
يك
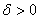 وجود داشته باشد كه
وجود داشته باشد كه
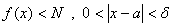 به طريق مشابه مي توان حد هاي زير را هم تعريف نمود :
به طريق مشابه مي توان حد هاي زير را هم تعريف نمود :
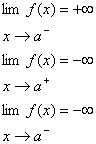
حال فرض كنيد
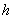 تابعي است
كه به صورت زير تعريف مي شود :
تابعي است
كه به صورت زير تعريف مي شود :
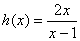
شكل زير نمودار اين تابع را نشان مي دهد:
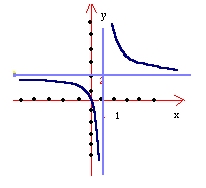
با
مراجعه به شكلهاي قبل تفاوت بين رفتار تابع رسم شده در شكل زير و توابع مربوط به
دو شكل ديگر را مورد توجه قرار مي دهيم . مشاهده مي كنيد كه
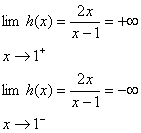
يعني در مورد تابع 3 وقتي با
مقادير كمتر از 1 به سمت 1 ميل ميكنند مقادير تابع بطور بيكران کاهش پيدا ميكند
و وقتي با مقادير بيشتر از 1 به سمت 1 ميل ميكنند مقادير تابع بطور بيكران افزايش
پيدا ميكند
قبل
از آوردن چند مثال
، به دو قضيه حدي در مورد حدهاي بينهايت نيازمنديم
قضيه حدي 14 : اگر
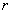 يك عدد
صحيح مثبت باشد ، انگاه
يك عدد
صحيح مثبت باشد ، انگاه
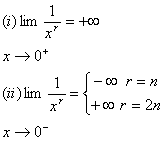
نمونه 1 : از قضيه حدي 14
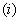 نتيجه مي شود كه
نتيجه مي شود كه
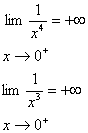
و از قضيه حدي 14
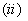 نتيجه مي شود كه
نتيجه مي شود كه
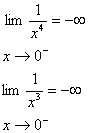
قضيه حدي 15 : فرض كنيد
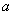 يك عدد حقيقي دلخواه
يك عدد حقيقي دلخواه
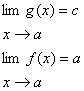
و
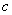 يك عدد ثابت ناصفر باشد ، آنگاه
يك عدد ثابت ناصفر باشد ، آنگاه
1 -
اگر
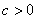 و اگر از طريق مقادير مثبت
و اگر از طريق مقادير مثبت
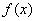 ،
،
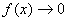 ، داريم
، داريم
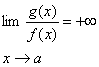
2 -
اگر
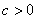 و اگر از طريق مقادير منفي
و اگر از طريق مقادير منفي
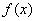 ,
,
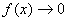 ، داريم
، داريم
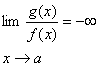
3 -
اگر
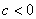 و اگر از طريق مقادير مثبت
و اگر از طريق مقادير مثبت
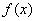 ،
،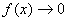 ، داريم
، داريم
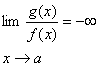
4 -
اگر
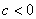 و اگر از طريق مقادير منفي
و اگر از طريق مقادير منفي
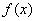 ،
،
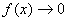 ، داريم
، داريم
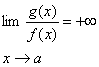
اگر
بجاي
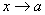 قرار دهيم
قرار دهيم
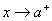 يا
يا
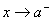 اين قضيه بازهم برقرار است .
اين قضيه بازهم برقرار است .
نمونه 2
الف
: براي محاسبه
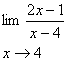 در اينجا
در اينجا
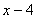 از طريق مقادير مثبت
به صفر ميل ميكند ملاحظه ميكنيد كه
از طريق مقادير مثبت
به صفر ميل ميكند ملاحظه ميكنيد كه
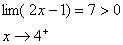 و
و
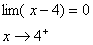 لذا
اگر قضيه حدي
12-1
رابكار ببريم داريم
لذا
اگر قضيه حدي
12-1
رابكار ببريم داريم
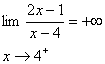
ب :
براي محاسبه
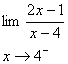 در اينجا
در اينجا
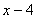 از طريق مقادير منفي
به صفر ميل ميكند ملاحظه ميكنيد كه
از طريق مقادير منفي
به صفر ميل ميكند ملاحظه ميكنيد كه
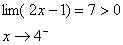 و
و
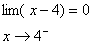 لذا
اگر قضيه حدي
12-2
رابكار ببريم داريم
لذا
اگر قضيه حدي
12-2
رابكار ببريم داريم
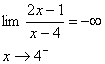
ج :
براي محاسبه
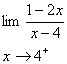 در اينجا
در اينجا
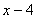 از طريق مقادير مثبت به صفر ميل ميكند ملاحظه
ميكنيد كه
از طريق مقادير مثبت به صفر ميل ميكند ملاحظه
ميكنيد كه
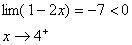 و
و
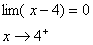 لذا
اگر قضيه حدي
12-3
رابكار ببريم داريم
لذا
اگر قضيه حدي
12-3
رابكار ببريم داريم
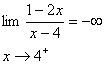
د :
براي محاسبه
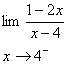 در اينجا
در اينجا
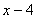 از طريق مقادير منفي
به صفر ميل ميكند
ملاحظه ميكنيد كه
از طريق مقادير منفي
به صفر ميل ميكند
ملاحظه ميكنيد كه
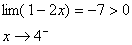 و
و
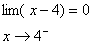 لذا اگر قضيه حدي
12-4
رابكار ببريم داريم
لذا اگر قضيه حدي
12-4
رابكار ببريم داريم
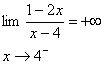
مثال 14 : مطلوب
است :
الف :
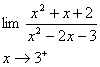
ب :
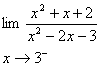
حل :
الف :
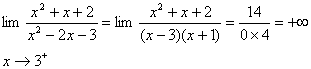
به آساني ثابت ميشود حد صورت برابر 14 است . در اين معادله حد مخرج برابر صفر است و مخرج با مقادير مثبت به صفر ميل ميكند و بنا بر قضيه حدي 12-1 حد تابع برابر است با
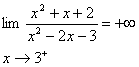
(ب) :
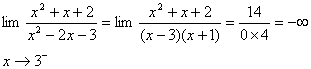
در اين حالت حد مخرج صفر است و مخرج با مقادير منفي
به 0 ميل ميكنيد بنابراين با توجه به قضيه حدي
12-3
داريم
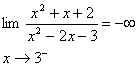
مثال 15 : مطلوب است
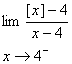
حل :
داريم
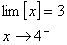 بنابراين نتيجه ميگيريم
بنابراين نتيجه ميگيريم
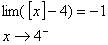 علاوه براين داريم
علاوه براين داريم
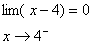 و
و
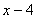 از طريق مقادير منفي به صفر ميل ميكند . پس بنا
به قضيه
12-4
حدي داريم :
از طريق مقادير منفي به صفر ميل ميكند . پس بنا
به قضيه
12-4
حدي داريم :
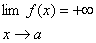
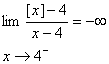
يادآوري ميكنيم كه چون
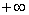 و
و
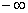 عدد نيستند ؛ قضاياي حدي ، براي حدهاي بینهايت
اعتبار ندارند . با اين وجود در مورد اين حدها ويژگيهاي زير برقرارند . اثبات آنها
براي تمرين واگذار ميشوند .
عدد نيستند ؛ قضاياي حدي ، براي حدهاي بینهايت
اعتبار ندارند . با اين وجود در مورد اين حدها ويژگيهاي زير برقرارند . اثبات آنها
براي تمرين واگذار ميشوند .
قضيه 16 : اگر
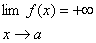 ,
,
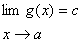 و
c
که
عدد دلخواه باشد انگاه
و
c
که
عدد دلخواه باشد انگاه
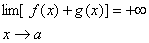 اگر
اگر
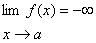 ,
,
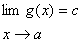 و c
عدد دلخواه باشد انگاه
و c
عدد دلخواه باشد انگاه
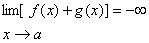
اگر بجای
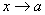 قرار دهیم
قرار دهیم
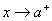 یا
یا
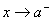 این قضیه
همچنان معتبر است
این قضیه
همچنان معتبر است
نمونه 3 : چون
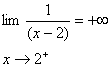 و
و
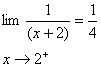 پس از قضیه های فوق
(i)
نتیجه می
شود که
پس از قضیه های فوق
(i)
نتیجه می
شود که
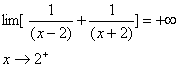
قضیه 17 : اگر
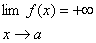 ,
,
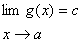 و a
یک عدد ثابت مخالف با
0
باشد , انگاه
اگر
و a
یک عدد ثابت مخالف با
0
باشد , انگاه
اگر
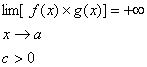
اگر
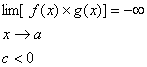
این قضیه برقرار است اگر بجای
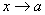 بنویسیم
بنویسیم
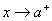 یا
یا
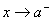
قضیه 18 : اگر
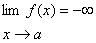 ,
,
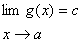 و
c
یک عدد ثابت مخالف با صفر باشد انگاه
اگر
و
c
یک عدد ثابت مخالف با صفر باشد انگاه
اگر
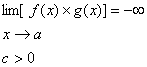
اگر
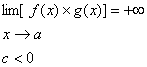
این قضیه همچنان برقرار است اگر به
جای
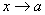 بنویسیم
بنویسیم
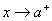 یا
یا
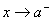 .
.
تعریف 3: خط
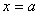 را یک مجانب قائم نمودار
را یک مجانب قائم نمودار
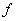 مینامند هرگاه دست کم یکی از
عبارتهای زیر درست شود باشد :
مینامند هرگاه دست کم یکی از
عبارتهای زیر درست شود باشد :
(I) اگر
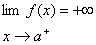
(II) اگر
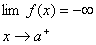
(III) اگر
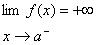
(IV) اگر
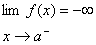
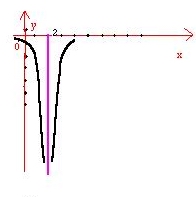
مثال 16 : مجانب قائم نمودار تابع تعریف شده توسط
معادله
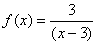 را بیابید و نمودار
را بیابید و نمودار
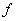 را رسم کنید
.
را رسم کنید
.
حل :
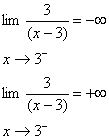
از تعریف نتیجه می شود که خط
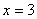 یک مجانب قائم نمودار
یک مجانب قائم نمودار
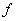 است نمودار
است نمودار
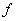 در شکل زیر نشان داده شده است .
در شکل زیر نشان داده شده است .
در تمرینهای زیر حد های خواسته شده
را محاسبه کنید .
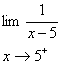
2.
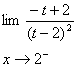
3.
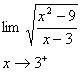
4.
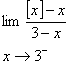
5.
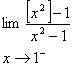
6.
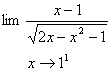
در تمرینات زیر مجانب نمودار تابع را
بیابید و نمودار آن را رسم کنید .
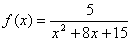
2.