مشتق / ماکزیمم و مینیمم توابع
قبلا دیده ایم که تعبیر هندسی مشتق یک تابع در یک نقطه عبارت است از ضریب زاویه خط مماس نمودار تابع در آن نقطه. این مطلب ما را قادر می سازد در رسم نمودار از مشتق کمک بگیریم.
مثلا برای تعیین نقاطی که در آنها خط مماس بر نمودار افقی است از مشتق می توان استفاده کرد, زیرا مشتق تابع در اینگونه نقاط برابر صفر است.
همچنین جهت تعیین بازه هایی که در آن بازه ها نمودار یک تابع بالای خط مماس است, و بازه هایی که در آن بازه ها نمودار پایین خط مماس قرار میگیرد,
میتوان از مشتق استفاده کرد. قبل از اینکه از مشتق برای رسم نمودار استفاده کنیم به چند تعریف و قضیه نیاز داریم.
تعریف 1 : گوییم تابع
 در
در
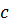 دارای یک مقدار ماکسیمم نسبی است اگر یک بازه باز شامل
دارای یک مقدار ماکسیمم نسبی است اگر یک بازه باز شامل
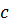 وجود داشته باشد که
وجود داشته باشد که
 روی آن تعریف بشود, و به ازای هر
روی آن تعریف بشود, و به ازای هر
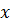 واقع در آن بازه, داشته باشیم
واقع در آن بازه, داشته باشیم
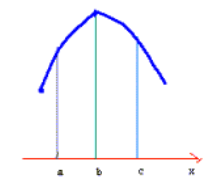
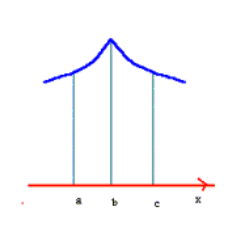
شکل زیر هر کدام قسمتی از نمودار یک تابع را نشان می دهد که دارای یک ماکسیمم نسبی است.
تعریف 2: گوییم تابع
 در
در
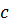 دارای یک مقدار مینیمم نسبی است اگر یک بازه باز شامل
دارای یک مقدار مینیمم نسبی است اگر یک بازه باز شامل
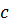 وجود داشته باشد که
وجود داشته باشد که
 روی آن تعریف بشود, و به ازای هر
روی آن تعریف بشود, و به ازای هر
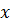 واقع در آن بازه, داشته باشیم
واقع در آن بازه, داشته باشیم
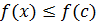
شکلهای زیر هر کدام قسمتی از نمودار تابعی را نشان می دهد که در
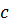 دارای یک مینیمم نسبی است. اگر تابع
دارای یک مینیمم نسبی است. اگر تابع
 در
در
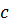 یک مقدار ماکسیمم نسبی با یک مقدار مینیمم نسبی داشته باشد, گوییم
یک مقدار ماکسیمم نسبی با یک مقدار مینیمم نسبی داشته باشد, گوییم
 در
در
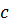 دارای یک اکسترمم نسبی است.
دارای یک اکسترمم نسبی است.
جهت پیدا کردن مقادیر ممکن
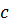 که به ازای آنها اکسترمم نسبی وجود داشته باشد, از قضیه زیر استفاده می شود.
که به ازای آنها اکسترمم نسبی وجود داشته باشد, از قضیه زیر استفاده می شود.
قضیه1: فرض کنید
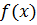 به ازای هر
به ازای هر
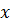 در بازه باز
در بازه باز
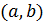 وجود داشته باشد و
وجود داشته باشد و
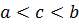 . اگر
. اگر
 در
در
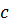 دارا یک اکسترمم نسبی باشد و
دارا یک اکسترمم نسبی باشد و
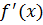 وجود داشته باشد, آنگاه .
وجود داشته باشد, آنگاه .
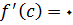
تعبیر هندسی قضیه این است که اگر
 در
در
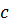 دارای یک اکسترمم نسبی باشد و نیز
دارای یک اکسترمم نسبی باشد و نیز
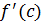 وجود داشته باشد, آنگاه نمودار
وجود داشته باشد, آنگاه نمودار
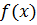 در نقطه
در نقطه
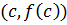 دارای یک خط مماس افقی است.
دارای یک خط مماس افقی است.
اگر
 یک تابع مشتق پذیر باشد, آنگاه تنها به ازای
یک تابع مشتق پذیر باشد, آنگاه تنها به ازای
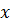 هایی که
هایی که
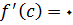 در انها مساوی با صفر است تابع
در انها مساوی با صفر است تابع
 ممکن است اکسترم نسبی داشته باشد, با وجود این ممکن هم هست که به ازای مقدار خاصی از
ممکن است اکسترم نسبی داشته باشد, با وجود این ممکن هم هست که به ازای مقدار خاصی از
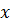 ,
,
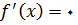 و در عین حال در آنجا دارای اکسترمم نباشد. این نکته در نمونه زیر نشان داده شده است.
و در عین حال در آنجا دارای اکسترمم نباشد. این نکته در نمونه زیر نشان داده شده است.
مثال 1 – فرض کنید تابع
 به صورت زیر تعریف شده است
به صورت زیر تعریف شده است
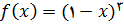
شکل زیر نمودار این تابع را نشان میدهد. داریم
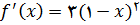 و بنا براین
و بنا براین
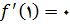 . اما برای
. اما برای
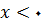 داریم
داریم
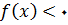 و برای
و برای
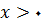 داریم
داریم
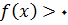 لذا در 1 اکسترمم نسبی ندارد.
لذا در 1 اکسترمم نسبی ندارد.
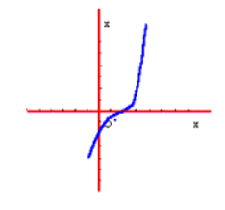
ممکن است تابعی مانند
 در عددی دارای اکسترمم نسبی باشد ولی
در عددی دارای اکسترمم نسبی باشد ولی
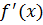 در آن عدد وجود نداشته باشد. این مورد در نمونه 2 نشان داده شده است.
در آن عدد وجود نداشته باشد. این مورد در نمونه 2 نشان داده شده است.
مثال 2 – فرض کنید تابع
 به صورت زیر تعریف شده باشد.
به صورت زیر تعریف شده باشد.
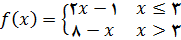
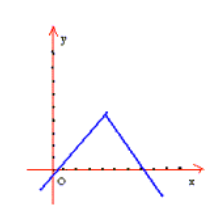
شکل زیر نمودار این تابع را نشان می دهد. تابع
 در 3 دارای یک ماکسیمم نسبی است. مشتق چپ در 3 برابر است با
در 3 دارای یک ماکسیمم نسبی است. مشتق چپ در 3 برابر است با
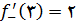 , و مشق راست در 3 برابر است با
, و مشق راست در 3 برابر است با
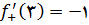 . پس نتیجه میگیریم که
. پس نتیجه میگیریم که
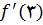 وجود ندارد.
وجود ندارد.
مثال 3 – نشان میدهد که چرا شرط
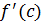 وجود داشته باشد, باید یکی از فرض های قضیه باشد.
پس به طور خلاصه, اگر به ازای عددی چون
وجود داشته باشد, باید یکی از فرض های قضیه باشد.
پس به طور خلاصه, اگر به ازای عددی چون
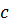 معیین باشد, یک شرط لازم برای اینکه
معیین باشد, یک شرط لازم برای اینکه
 در
در
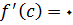 دارای اکسترمم نسبی باشد این است که با
دارای اکسترمم نسبی باشد این است که با
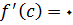 ؛ و یا
؛ و یا
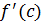 وجود نداشته باشد. اما این شرط کافی نیست.
وجود نداشته باشد. اما این شرط کافی نیست.
تعریف 3: اگر عددی از قلمرو تابع
 باشد. گوییم
باشد. گوییم
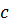 یک عدد بحرانی است هرگاه یا
یک عدد بحرانی است هرگاه یا
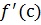 و یا
و یا
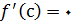 وجود نداشته باشد. طبق این تعریف و بحث قبلی, یک شرط لازم برای اینکه تابعی در عددی چون
وجود نداشته باشد. طبق این تعریف و بحث قبلی, یک شرط لازم برای اینکه تابعی در عددی چون
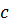 دارای یک اکسترمم نسبی باشد این است که یک عدد بحرانی
دارای یک اکسترمم نسبی باشد این است که یک عدد بحرانی
 باشد.
باشد.
مثال 4 – تابع
 به صورت
به صورت
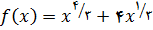 داده شده است. اعداد بحرانی
داده شده است. اعداد بحرانی
 را پیدا کنید.
را پیدا کنید.
حل:
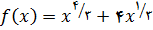
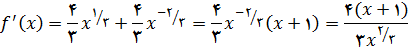
پس
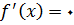 وقتی که
وقتی که
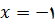 , و برای
, و برای
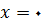 ,
,
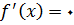 وجود ندارد.
وجود ندارد.
تعریف4: گوییم تابع
 بر بازه ای دارای یک مقدار ماکزیمم مطلق است هرگاه عددی مانند
بر بازه ای دارای یک مقدار ماکزیمم مطلق است هرگاه عددی مانند
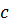 در آن بازه باشد که به ازای هر
در آن بازه باشد که به ازای هر
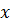 متعلق به آن بازه داشته باشیم
متعلق به آن بازه داشته باشیم
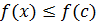 در این صورت مقدار ماکسیمم مطلق
در این صورت مقدار ماکسیمم مطلق
 روی آن بازه
روی آن بازه
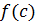 است.
است.
تعریف 5: گوییم تابع
 بر بازه ای دارای یک مقدار مینمم مطلق است هرگاه عددی مانند
بر بازه ای دارای یک مقدار مینمم مطلق است هرگاه عددی مانند
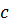 در آن بازه باشد که به ازای هر
در آن بازه باشد که به ازای هر
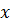 متعلق به ان بازه داشته باشیم
متعلق به ان بازه داشته باشیم
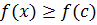 . در این صورت مقدار مینیمم مطلق
. در این صورت مقدار مینیمم مطلق
 روی آن بازه
روی آن بازه
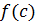 است.
است.
اکسترمم مطلق یک تابع در یک بازه, ماکزیمم مطلق و یا مینیم مطلق آن تابع روی آن بازه است.
یک تابع ممکن است دارای اکسترمم مطلق باشد یا نباشد. در نمونه های زیر تابع و یک بازه داده شده اند و اکسترمم ها مطلق درصورت وجود تعیین می شوند.
مثال 5 – فرض کنید تابع
 به صورت زیر تعریف شده باشد
به صورت زیر تعریف شده باشد
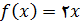
شکل زیر نمودار
 روی بازه
روی بازه
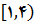 را نمایش میدهد.
را نمایش میدهد.
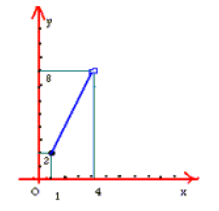
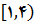 تابع, مقدار مینیمم مطلقی برابر با 2 دارد. اما
تابع, مقدار مینیمم مطلقی برابر با 2 دارد. اما
 بر
بر
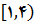 مقدار ماکزیمم مطلق ندارد,
مقدار ماکزیمم مطلق ندارد,
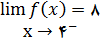
, ولی روی بازه مفروض,
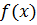 همواره کمتر از 8 است.
همواره کمتر از 8 است.
مثال 6 – تابع
 به صورت زیر تعریف شده است
به صورت زیر تعریف شده است
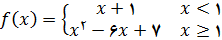
نمودار
 بر
بر
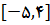 در شکل زیر رسم شده است. مقدار ماکزیمم مطلق
در شکل زیر رسم شده است. مقدار ماکزیمم مطلق
 روی
روی
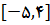 به ازای 1 به دست می آید و
به ازای 1 به دست می آید و
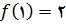 به مقدار مینیمم مطلق
به مقدار مینیمم مطلق
 روی
روی
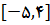 به ازای
به ازای
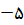 به دست می آید و
به دست می آید و
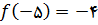 . دقت کنید که
. دقت کنید که
 در 1 دارای یک مقدار ماکسیمم نسبی و در 3 دارای یک مقدار مینیمم نسبی است.
همچنین مشاهده کنید که 1 یک عدد بحرانی
در 1 دارای یک مقدار ماکسیمم نسبی و در 3 دارای یک مقدار مینیمم نسبی است.
همچنین مشاهده کنید که 1 یک عدد بحرانی
 است زیرا
است زیرا
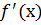 در 1 وجود ندارد 3 یک عدد بحرانی است زیرا
در 1 وجود ندارد 3 یک عدد بحرانی است زیرا
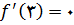
تعریف 6: گوییم
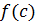 مقدار ماکسیمم مطلق تابع
مقدار ماکسیمم مطلق تابع
 است هرگاه
است هرگاه
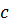 در قلمرو
در قلمرو
 باشد و به ازای هر
باشد و به ازای هر
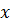 در قلمرو
در قلمرو
 ,
,
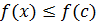
تعریف 7: گوییم
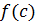 مقدار مینیمم مطلق تابع
مقدار مینیمم مطلق تابع
 است هرگاه
است هرگاه
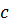 در قلمرو
در قلمرو
 باشد و به ازای هر
باشد و به ازای هر
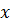 در قلمرو
در قلمرو
 ,
,
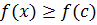
مثال 7 – نمودار تابع
 با ضابطه
با ضابطه
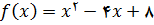 یک سهمی است که در شکل زیر رسم شده است. پائین ترین نقطه سهمی
یک سهمی است که در شکل زیر رسم شده است. پائین ترین نقطه سهمی
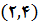 است و دهانه آن به طرف بالا است. تابع دارای مقدار مینیمم مطلقی برابر 4 است
که به ازای 2 به دست می آید .
است و دهانه آن به طرف بالا است. تابع دارای مقدار مینیمم مطلقی برابر 4 است
که به ازای 2 به دست می آید .
 ماکسیمم مطلق ندارد.
ماکسیمم مطلق ندارد.
با مراجعه به نمونه های قبلی میبینیم تنها موردی که هم مقدار ماکسیمم مطلق و هم مقدار مینیمم مطلق وجود دارد نمونه 6 است که در آن تابع روی بازه بسته
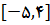 پیوسته است در نمونه های دیگر یا بازه بسته نیست
یا اگر تابعی روی بازه بسته ای پیوسته باشد, قضیه ای بنام اکسترمم تضمین میکند که روی آن بازه تابع هم یک مقدار ماکسیمم مطلق دارد و هم یک مقدار مینیمم مطلق.
پیوسته است در نمونه های دیگر یا بازه بسته نیست
یا اگر تابعی روی بازه بسته ای پیوسته باشد, قضیه ای بنام اکسترمم تضمین میکند که روی آن بازه تابع هم یک مقدار ماکسیمم مطلق دارد و هم یک مقدار مینیمم مطلق.
قضیه2 (قضیه اکسترمم): اگر تابع
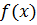 روی بازه بسته
روی بازه بسته
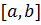 پیوسته باشد, انگاه روی
پیوسته باشد, انگاه روی
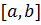 یک مقدار ماکسیمم مطلق و یک مقدار مینیمم مطلق دارد.
یک مقدار ماکسیمم مطلق و یک مقدار مینیمم مطلق دارد.
قضیه 3: حاکی از آن است که پیوستگی یک تابع روی یک بازه بسته, شرطی است کافی برای تضمین این نکته که تابع روی آن بازه هم مقدار ماکسیمم مطلق داشته باشد و هم مقدار مینیمم مطلق.
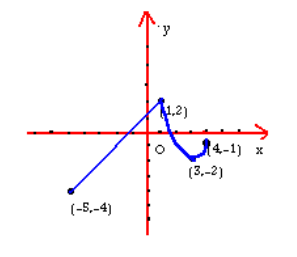
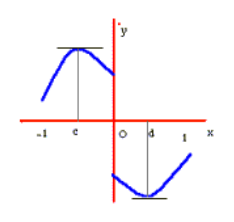
با این وجود, این شرط یک شرط لازم نیست. مثلا, تابعی که نمودارش در شکل زیر رسم شده است, گرچه روی بازه باز
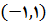 ناپیوسته است ولی در
ناپیوسته است ولی در
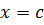 یک مقدار ماکسیمم مطلق دارد. و یک مقدار مینیمم مطلق هم در
یک مقدار ماکسیمم مطلق دارد. و یک مقدار مینیمم مطلق هم در
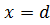 دارد.
دارد.
اکسترمم مطلق یک تابع که بر یک بازه بسته پیوسته است باید یک اکسترمم نسبی باشد و یا مقدار تابع به ازای یکی از نقاط انتهایی بازه. چون یک شرط لازم برای اینکه تابعی در عددی مثل
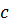 یک اکسترمم نسبی داشته باشد, این است که
یک اکسترمم نسبی داشته باشد, این است که
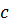 یک عدد بحرانی تابع باشد.
یک عدد بحرانی تابع باشد.
پس مقدار ماکسیمم مطلق و مقدار مینیمم مطلق یک تابع پیوسته
 روی یک بازه بسته
روی یک بازه بسته
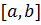 را می توان با دستور العمل زیر به دست اورد:
را می توان با دستور العمل زیر به دست اورد:
1. مقدار تابع را به ازای اعداد
 روی
روی
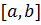 به دست اورید.
به دست اورید.
2. مقادیر
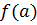 و
و
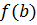 را بیابید. بزرگترین مقدار به دست امده در مراحل 1و 2
مقدار ماکسیمم مطلق و کوچکترین مقدار به دست آمده در مراحل 1 و 2 مثدار مینیمم مطلق است.
را بیابید. بزرگترین مقدار به دست امده در مراحل 1و 2
مقدار ماکسیمم مطلق و کوچکترین مقدار به دست آمده در مراحل 1 و 2 مثدار مینیمم مطلق است.
مثال 8: اگر
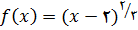 اکسترمم های مطلق
اکسترمم های مطلق
 روی
روی
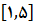 را به دست اورید.
را به دست اورید.
حل: چون
 بر
بر
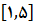 پیوسته است قضیه اکسترمم را مورد استفاده قرار می دهیم.
پیوسته است قضیه اکسترمم را مورد استفاده قرار می دهیم.
هیچ
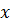 وجود ندارد که به ازای آن
وجود ندارد که به ازای آن
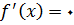 . با این وجود چون
. با این وجود چون
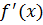 در 2 وجود ندارد, نتیجه میگیریم که 2 یک عدد بحرانی
در 2 وجود ندارد, نتیجه میگیریم که 2 یک عدد بحرانی
 است. پس اکسترمم های مطلق یا به ازای 2 ,
یا به ازای یکی از نقاط انتهایی بازه به دست می آید. مقادیر تابع به ازای اعداد فوق در جدول زیر آمده اند. با توجه به جدول, نتیجه میگیریم که مقدار مینیمم
است. پس اکسترمم های مطلق یا به ازای 2 ,
یا به ازای یکی از نقاط انتهایی بازه به دست می آید. مقادیر تابع به ازای اعداد فوق در جدول زیر آمده اند. با توجه به جدول, نتیجه میگیریم که مقدار مینیمم
 روی
روی
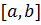 برابر صفر است که به ازای 5 به دست می آید و مقدار ماکسیمم مطلق
برابر صفر است که به ازای 5 به دست می آید و مقدار ماکسیمم مطلق
 رو
رو
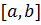 برابر
برابر
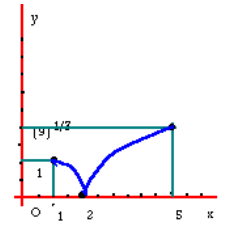
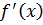 است که به ازای 5 به دست می آید نمودار تابع بر
است که به ازای 5 به دست می آید نمودار تابع بر
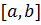 در شکل زیر رسم شده است.
در شکل زیر رسم شده است.
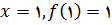
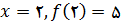
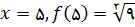
در تمرین های زیر اعداد بحرانی تابع داده شده را پیدا کنید
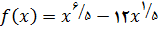
2.
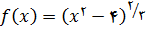
3.
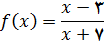
4.
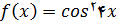
5.
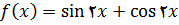
در تمرین های زیر, اکسترممهای مطلق تابع مفروض روی بازه داده شده را, درصورت وجود, بیابید و تعیین کنید به ازای چه مقادیری از
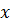 این اکسترمم های مطلق به دست می آیند. نمودار تابع روی بازه مفروض را رسم کنید.
این اکسترمم های مطلق به دست می آیند. نمودار تابع روی بازه مفروض را رسم کنید.
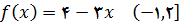
7.
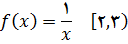
8.
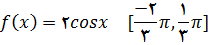
9.
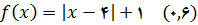
10.
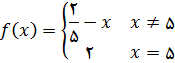
11.
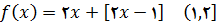
در تمرین های زیر, با روشی گه در مثالهای این بخش مورد استفاده قرار گرفت, مقادیر ماکسیمم و مینیمم مطلق تابع مفروض بر بازه داده شده را محاسبه, و نمودار تابع بر آن بازه را رسم کنید.
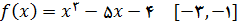
13.
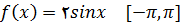
14.