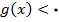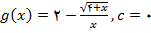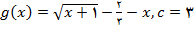ریاضی عمومی / پیوستگی تابع در یک عدد( نقطه)
فرض کنید که توابع
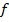 و
و
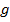 و
و
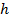 و روی بازه
و روی بازه
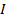 ی شامل
ی شامل
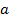 احتمالا بجز خود
احتمالا بجز خود
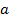 تعریف شده باشند و به ازای هر
تعریف شده باشند و به ازای هر
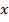 در
در
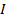 که
که
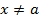 داشته باشیم
داشته باشیم
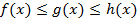
. همچنین فرض کنید که هر دوی
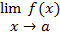 و
و
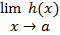 موجود و برابر
موجود و برابر
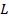 باشند . آنگاه
باشند . آنگاه
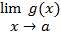 موجود و برابر با
موجود و برابر با 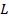 است.
اکنون به بحث درباره چهار قضیه میپردازیم که برای اثبات چند قضیه مهم در بخشهای آینده مورد نیازند .
است.
اکنون به بحث درباره چهار قضیه میپردازیم که برای اثبات چند قضیه مهم در بخشهای آینده مورد نیازند .
قضیه 1 : اگر
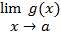 موجود و مثبت باشد , انگاه یک بازه باز شامل
موجود و مثبت باشد , انگاه یک بازه باز شامل
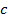 وجود دارد که برای هر
وجود دارد که برای هر
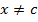 واقع در آن بازه
داریم .
واقع در آن بازه
داریم .
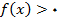
نمونه 1 : تابع f را که به صورت زیر تعریف می شوند در نظر بگیرید .
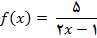 چون
چون
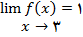 و
و
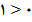 پس بنا به قضیه 1 یک بازه باز شامل 3 وجود دارد که برای هر
پس بنا به قضیه 1 یک بازه باز شامل 3 وجود دارد که برای هر
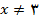 واقع در آن بازه داریم
واقع در آن بازه داریم
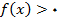 , مثلا بازه
, مثلا بازه
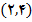 چنین بازه ای است. در واقع هر بازه باز که
چنین بازه ای است. در واقع هر بازه باز که
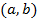 برای ان داشته باشیم
برای ان داشته باشیم
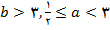 چنین است.
چنین است.
نمونه 2 : فرض کنید
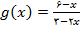 شکل زیر نمودار را نشان میدهد
شکل زیر نمودار را نشان میدهد
داریم
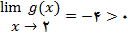 پس بنا به قضیه فوق, یک بازه باز شامل 2 وجود دارد که برای هر
پس بنا به قضیه فوق, یک بازه باز شامل 2 وجود دارد که برای هر
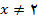 واقع در آن بازه ,
واقع در آن بازه ,
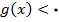 مثلا
مثلا
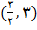 چنین بازه ای است. به طور کلی هر بازه باز
چنین بازه ای است. به طور کلی هر بازه باز
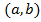 که در آن
که در آن
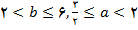 چنین است.
چنین است.
قضیه 2: فرض کنید تابع
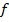 روی بازه باز
روی بازه باز
 که شامل عدد
که شامل عدد
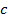 است , بجز احتمالا در خود
است , بجز احتمالا در خود
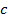 تعریف شده است. همچنین فرض کنید عدد
تعریف شده است. همچنین فرض کنید عدد
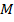 ی وجود دارد که برای آن یک عدد
ی وجود دارد که برای آن یک عدد
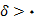 یافت می شود که وقتی
یافت می شود که وقتی
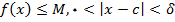 در اینصورت, اگر
در اینصورت, اگر
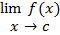 موجود و برابر با
موجود و برابر با
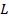 یا هر دو منفی باشند. دو حالت درنظر میگیریم.
یا هر دو منفی باشند. دو حالت درنظر میگیریم.
حالت 1:
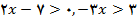 یعنی
یعنی
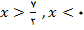 . هیچ مقدار از
. هیچ مقدار از
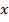 وجود ندارد که هر دوی این نامساویها به ازای آن برقرار باشند, بنابراین مجموعه جواب حالت 1 , مجموعه تهی است.
وجود ندارد که هر دوی این نامساویها به ازای آن برقرار باشند, بنابراین مجموعه جواب حالت 1 , مجموعه تهی است.
حالت 2:
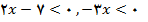 بنابراین مجموعه جواب حالت 2 بازه
بنابراین مجموعه جواب حالت 2 بازه
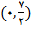 است پس
نامساوی (4) برقرار است اگر
است پس
نامساوی (4) برقرار است اگر
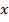 در بازه باز
در بازه باز
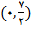 باشد. نتیجه میگیریم که در هر بازه باز
باشد. نتیجه میگیریم که در هر بازه باز
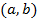 که برای آن داشته باشیم
که برای آن داشته باشیم
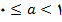 و
و
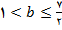 بازه ای است که شامل 1 است و برای هر
بازه ای است که شامل 1 است و برای هر
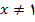 در چنین بازه ای
در چنین بازه ای
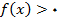 به خصوص بازه
به خصوص بازه
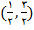 چنین است.
چنین است.
قضیه 3: اگر
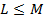 موجود و منفی باشند , آنگاه یک بازه باز شامل
موجود و منفی باشند , آنگاه یک بازه باز شامل
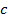 وجود دارد که برای هر
وجود دارد که برای هر
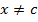 واقع در این بازه داریم
واقع در این بازه داریم
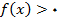 باشد
باشد
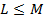 .
.
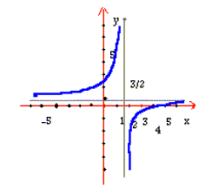
نمونه 3 :در شکل زیر نمودار تابعی مانند
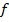 نشان داده شده که شرایط قضیه را بر آورده میکند . از شکل مشاهده می شود که
نشان داده شده که شرایط قضیه را بر آورده میکند . از شکل مشاهده می شود که
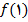 تعریف نشده ولی تابع روی بازه باز
تعریف نشده ولی تابع روی بازه باز
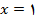 بجز در
بجز در
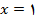 تعریف شده است. به علاوه اگر
تعریف شده است. به علاوه اگر
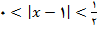 آنگاه
آنگاه
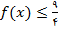 .
از اینرو , از قضیه نتیجه می شود که اگر
.
از اینرو , از قضیه نتیجه می شود که اگر
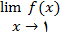 موجود و برابر
موجود و برابر
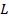 باشد, آنگاه
باشد, آنگاه
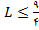 .
در شکل مشاهده می شود که
.
در شکل مشاهده می شود که
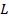 وجود دارد و برابر عدد 2 است .
وجود دارد و برابر عدد 2 است .
قضیه 4: فرض کنید تابع
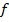 روی بازه باز
روی بازه باز
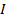 شامل عدد
شامل عدد
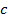 است بجز احتمالا خود
است بجز احتمالا خود
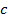 , تعریف شده است. همچنین فرض کنید عدد
, تعریف شده است. همچنین فرض کنید عدد
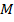 وجود دارد که به ازای آن یک عدد
وجود دارد که به ازای آن یک عدد
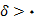 پیدا میشود که وقتی
پیدا میشود که وقتی
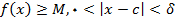 در اینصورت, اگر
در اینصورت, اگر
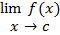 موجود و برابر با عدد
موجود و برابر با عدد
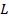 باشد خواهیم داشت
باشد خواهیم داشت 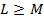 .
.
در تمرین های زیر یک تابع
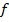 و یک عدد
و یک عدد
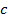 داده شده است
داده شده است
الف:
نشان دهید که
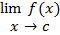
ب: قضیه را در مورد تابع
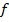 بررسی کنید به این منظور یک بازه باز شامل
بررسی کنید به این منظور یک بازه باز شامل
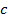 بیابید که به ازای هر
بیابید که به ازای هر
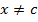 در آن بازه داشته باشیم
در آن بازه داشته باشیم 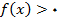 .
.
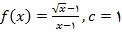
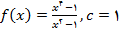
2 – در تمرین های زیر یک تابع
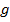 و یک عدد
و یک عدد
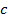 داده شده است
داده شده است
الف: نشان دهید که
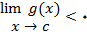
ب: قضیه را در مورد تابع
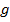 بررسی کنید به این منظور یک بازه شامل
بررسی کنید به این منظور یک بازه شامل
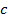 بیابید که به ازای هر
بیابید که به ازای هر
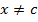 در آن بازه
در آن بازه