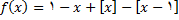ریاضی عمومی / پیوستگی تابع در یک عدد( نقطه)
در بخش قبل تابع
 را که به صورت
را که به صورت
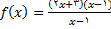 تعریف شده بود, درنظر گرفتیم تابع
تعریف شده بود, درنظر گرفتیم تابع
 برای تمام مقادیر
برای تمام مقادیر
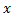 بجز 1 معین است. شکل زیر نمودار
بجز 1 معین است. شکل زیر نمودار  را نشان میدهد
را نشان میدهد
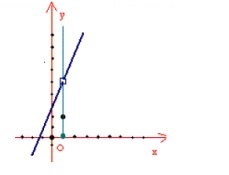
این نمودار از تمام نقاط خط
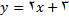 بجز نقطه
بجز نقطه
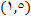 تشکیل شده است. مشاهده میشود که در نقطه
تشکیل شده است. مشاهده میشود که در نقطه 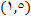 یک شکستگی در نمودار
یک شکستگی در نمودار
 وجود دارد و گوییم که تابع
وجود دارد و گوییم که تابع
 در نقطه به طول 1 ناپیوسته است. حال اگر تعریف کنیم که
در نقطه به طول 1 ناپیوسته است. حال اگر تعریف کنیم که
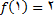 تابع
تابع
 برای تمام مقادیر
برای تمام مقادیر 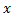 تعریف شده باشد ولی باز هم در نمودار تابع یک شکستگی وجود دارد و هنوز هم تابع
تعریف شده باشد ولی باز هم در نمودار تابع یک شکستگی وجود دارد و هنوز هم تابع
 در بازه 1 ناپیوسته است ولی اگر
در بازه 1 ناپیوسته است ولی اگر
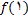 را برابر 5 تعریف کنیم, دیگر در نمودار شکستگی وجود ندارد و گوییم تابع به ازای تمام مقادیر پیوسته است.
را برابر 5 تعریف کنیم, دیگر در نمودار شکستگی وجود ندارد و گوییم تابع به ازای تمام مقادیر پیوسته است.
تعریف 1 : تابع  را در عدد
را در عدد
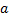 پیوسته گوییم اگر و تنها اگر سه شرط زیر برقرار باشد:
پیوسته گوییم اگر و تنها اگر سه شرط زیر برقرار باشد:
1 - 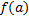 وجود داشته باشد
وجود داشته باشد
2 - 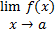 وجود داشته باشد
وجود داشته باشد
3 - 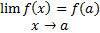
اگر یک یا چند شرط از شرایط فوق برقرار باشد, گوییم تابع f در a پیوسته است.
اکنون چند نمونه از توابع ناپیوسته را بررسی میکنیم. در هرنمونه, نمودار تابع را رسم کرده نقاط شکستگی نمودار را تعین میکنیم و نشان میدهیم که در هر ناپیوستگی, کدامیک از سه شرط فوق برقرار نیست.
نمونه 1 : فرض کنید تابع  به صورت زیر تعریف شده است.
به صورت زیر تعریف شده است.
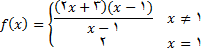
شکل زیر نمودار این تابع را نشان میدهد. مشاهده میشود که یک شکستگی در نمودار در نقطه
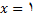 وجود دارد
وجود دارد

حال سه شرط تعریف فوق را بیان میکنیم.
1 - داریم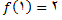 , بنابراین شرط 1 برقرار است
, بنابراین شرط 1 برقرار است
2 - داریم 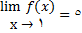 , بنابراین شرط 2برقرار است.
, بنابراین شرط 2برقرار است.
3 - داریم 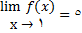 , اما
, اما
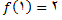 , بنابراین شرط3 برقرار نیست.
, بنابراین شرط3 برقرار نیست.
پس تابع در نقطه ای به طول 1 ناپیوسته است.
دقت کنید که اگر در نمونه1 , 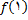 رابرابر 5 تعریف کنیم , انگاه
رابرابر 5 تعریف کنیم , انگاه
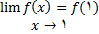 , و تابعf در 1 پیوسته خواهد بود..
, و تابعf در 1 پیوسته خواهد بود..
نمونه 2: فرض کنید تابع 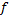 به صورت
به صورت
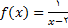 تعریف شده است را درنظر بگیرید. شکل زیر نمودار تابع
تعریف شده است را درنظر بگیرید. شکل زیر نمودار تابع
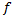 را نشان میدهد.
را نشان میدهد.
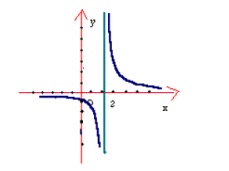
در نمودار 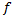 در نقطه به طول 2 شکستگی وجود دارد. حال سه شرط تعریف را بررسی میکنیم. چون
در نقطه به طول 2 شکستگی وجود دارد. حال سه شرط تعریف را بررسی میکنیم. چون
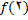 تعریف شده است , شرط 1برقرار نیست و بنابراین, تابع در 2 ناپیوسته است.
تعریف شده است , شرط 1برقرار نیست و بنابراین, تابع در 2 ناپیوسته است.
نمونه 3: فرض کنید تابع 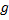 به صورت زیر تعریف شده است.
به صورت زیر تعریف شده است.
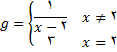
نمودار 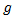 در شکل زیر تعریف شده است .
در شکل زیر تعریف شده است .
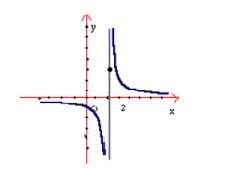
سه شرط تعریف را در عدد 2 بررسی میکنیم
1- 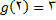 لذا شرط 1 برقرار است.
لذا شرط 1 برقرار است.
2 - 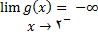 و
و
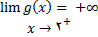 بنابراین , شرط 2 برقرار نیست. لذا
بنابراین , شرط 2 برقرار نیست. لذا
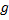 در 2 ناپیوسته است.
در 2 ناپیوسته است.
نمونه 4: فرض کنید
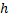 به صورت
به صورت 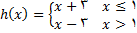 شکل زیر نمودار معادله را نشان میدهد.
شکل زیر نمودار معادله را نشان میدهد.
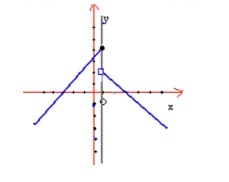
چون در نمودار در نقطه 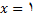 شکستگی وجود دارد. سه شرط تعریف را برای
شکستگی وجود دارد. سه شرط تعریف را برای
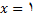 بررسی میکنیم .
بررسی میکنیم .
1 - 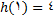 بنابراین شرط 1برقرار است .
بنابراین شرط 1برقرار است .
2 - 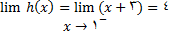 و
و
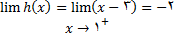 چون
چون
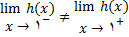 نتیجه میگیریم که
نتیجه میگیریم که
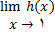 وجود ندارد از اینرو شرط 2بنابراین تابع
وجود ندارد از اینرو شرط 2بنابراین تابع
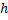 در1 ناپیوسته است
در1 ناپیوسته است
بعد از نمونه 1 تذکر دادیم که اگر
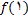 را برابر 5 تعریف کنیم انگاه تابع
را برابر 5 تعریف کنیم انگاه تابع
 در عدد 1 پیوسته خواهد بود. این مطلب مفهوم ناپیوستگی رفع شدنی را نشان میدهد.
در عدد 1 پیوسته خواهد بود. این مطلب مفهوم ناپیوستگی رفع شدنی را نشان میدهد.
به طور کلی فرض کنید
 تابعی است که در عدد
تابعی است که در عدد
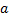 ناپیوسته است ولی
ناپیوسته است ولی
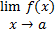 وجود دارد. در اینصورت
وجود دارد. در اینصورت
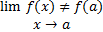 و یا
و یا
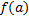 وجود ندارد. یک چنین ناپیوستگی را رفع شدنی میگوییم زیرا اگر
وجود ندارد. یک چنین ناپیوستگی را رفع شدنی میگوییم زیرا اگر
 را در
را در
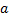 طوری تعریف کنیم که
طوری تعریف کنیم که
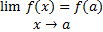 بنابراین تابع مورد نظر در
بنابراین تابع مورد نظر در
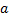 پیوسته می شود. اگر ناپیوستگی رفع شدنی نباشد آنرا ناپیوستگی اساسی مینامیم.
پیوسته می شود. اگر ناپیوستگی رفع شدنی نباشد آنرا ناپیوستگی اساسی مینامیم.
قضایایی درباره پیوستگی
با استفاده از تعریف و قضایای حدی قضیه زیر در مورد توابعی که در یک عدد پیوسته هستند به دست میآید.
قضیه 1 : اگر توابع
 و
و
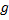 در عدد
در عدد 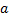 پیوسته باشند انگاه
پیوسته باشند انگاه
1 - تابع 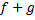 در
در 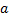 پیوسته است.
پیوسته است.
2 - تابع 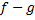 در
در 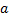 پیوسته است.
پیوسته است.
3 - تابع 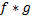 در
در 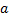 پیوسته است.
پیوسته است.
4 - تابع  در
در 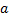 پیوسته است به شرطی که
پیوسته است به شرطی که 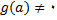
برای نشان دادن نوع اثباتی که برای هر قسمت این قضیه لازم است 1 را ثابت میکنیم. چون  و
و 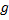 در عدد
در عدد 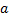 پیوسته هستند بنا به تعریف داریم
پیوسته هستند بنا به تعریف داریم
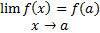 (1)
(1)
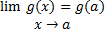 (2)
(2)
بنا براین طبق قضیه حدی 1 و معادلات (1) و (2) داریم
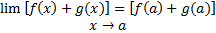 (3)
(3)
اما معادله (3) شرط پیوستگی 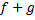 در
در
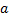 است و بنابران اثبات قسمت به انجام میرسد.
است و بنابران اثبات قسمت به انجام میرسد.
قضیه 2 : تابع چند جمله ای در هر عدد پیوسته است.
مثال 1 : اگر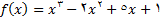 انگاه
انگاه
 یک تابع چند جمله ای است و بنابراین با استناد به قضیه فوق در هر عددی پیوسته است.
یک تابع چند جمله ای است و بنابراین با استناد به قضیه فوق در هر عددی پیوسته است.
قضیه 3: تابع گویا در هر عدد از قلمرو خود پیوسته است.
مثال 2 : فرض کنید 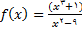 همه مقادیری از
همه مقادیری از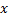 را بیابید که به ازای انها
را بیابید که به ازای انها  پیوسته است.
پیوسته است.
حل: قلمرو  مجموعه همه اعداد حقیقی است بجز اعدادی که به ازای انها
مجموعه همه اعداد حقیقی است بجز اعدادی که به ازای انها
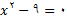 چون
چون
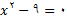 وقتی
وقتی
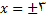 نتیجه می شود که قلمرو مجموعه
نتیجه می شود که قلمرو مجموعه
 همه اعداد حقیقی بجز
همه اعداد حقیقی بجز 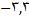 است.
است.
قضیه 4 : فرض کنید 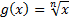 و
و 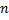 عددی صحیح مثبت و دلخواهی است.
در اینصورت
عددی صحیح مثبت و دلخواهی است.
در اینصورت 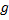 در
در
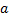 پیوسته است اگر یکی از دو حالت زیر برقرار باشد.
پیوسته است اگر یکی از دو حالت زیر برقرار باشد.
1 - 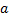 عدد مثبت و دلخواهی باشد.
عدد مثبت و دلخواهی باشد.
2 - 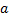 عددی منفی dا صفر باشد و
عددی منفی dا صفر باشد و
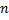 فرد باشد.
فرد باشد.
مثال 3:
(الف) اگر 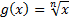 انگاه از قضیه قبلی فرمول 1 نتیجه می شود که
انگاه از قضیه قبلی فرمول 1 نتیجه می شود که
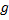 به ازای هر عدد مثبتی پیوسته است.
به ازای هر عدد مثبتی پیوسته است.
ب) اگر 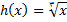 از قضیه 4 بخش 1 و 2 نتیجه می شود که
از قضیه 4 بخش 1 و 2 نتیجه می شود که 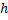 به ازای هر عدد حقیقی پیوسته است.
به ازای هر عدد حقیقی پیوسته است.
قضیه 5: تابع  در
در 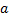 پیوسته است اگر
پیوسته است اگر  در یک بازه شامل
در یک بازه شامل
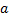 تعریف شده باشد و برای هر
تعریف شده باشد و برای هر
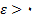 یک
یک
 وجود داشته باشدکه وقتی
وجود داشته باشدکه وقتی
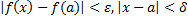 این قضیه برای اثبات قضیه مهم زیر در مورد حد تابع مرکب به کار میرود.
این قضیه برای اثبات قضیه مهم زیر در مورد حد تابع مرکب به کار میرود.
قضیه6 : اگر داشته باشیم
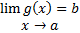
اگر تابع
 در
در
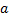 پیوسته باشد.
انگاه
پیوسته باشد.
انگاه
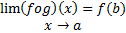
و به عبارت دیگر
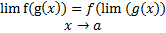
مثال 4:با استفاده از قضیه حدی 6 حد زیر را بیابید.
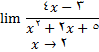
حل: درابتدا تابع موجود را به صورت دو تابع 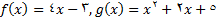 در نظر میگیریم حال
در نظر میگیریم حال 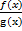 را به صورت حاصلضرب
را به صورت حاصلضرب
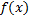 و
و
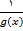 در نظر میگیریم و قضیه حدی 6 ( درمورد حاصلضرب) را به کار می بریم. قبل از هرچیز باید
در نظر میگیریم و قضیه حدی 6 ( درمورد حاصلضرب) را به کار می بریم. قبل از هرچیز باید
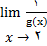
را پیدا کنیم. برای این کار
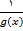 را به صورت مقدار یک تابع مرکب درنظر میگیریم . اگر تابع
را به صورت مقدار یک تابع مرکب درنظر میگیریم . اگر تابع 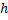 به صورت
به صورت 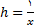 تعریف شده باشد آنگاه تابع مرکب
تعریف شده باشد آنگاه تابع مرکب
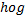 به صورت
به صورت
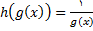
تعریف میشود. اما داریم
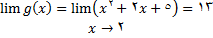
برای استفاده از قضیه تابع باید در عدد 13 پیوسته باشد که درستی این موضوع از قضیه نتیجه میشود پس
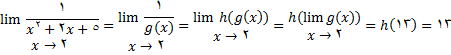
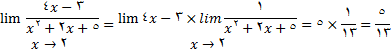
قضیه حدی 7 : اگر
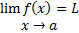
و اگر
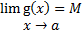
و
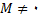 آنگاه
آنگاه
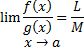
مثال 5: حد زیر را محاسبه کنید
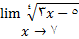
حل: فرض میکنیم توابع  و
و
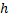 به صورت زیر تعریف شده اند
به صورت زیر تعریف شده اند
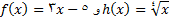 در اینصورت تابع مرکب
در اینصورت تابع مرکب 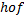 به صورت زیر تعریف می شود.
به صورت زیر تعریف می شود.
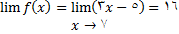
پس برای استفاده از قضیه در مورد تابع مرکب 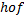 باید در 16 پیوسته باشد که صحت این امر از قضیه نتیجه میشود پس راه حل به این صورت است
باید در 16 پیوسته باشد که صحت این امر از قضیه نتیجه میشود پس راه حل به این صورت است
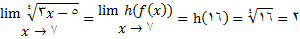
قضیه حدی 8: اگر
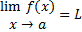
انگاه
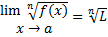
که در آن اگر 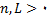 هر عدد طبیعی می تواند باشد و اگر
هر عدد طبیعی می تواند باشد و اگر
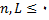 عدد صحیح فرد مثبتی است.
عدد صحیح فرد مثبتی است.
قضیه حدی 9 : اگر تابع 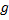 در
در
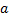 پیوسته باشد و تابع
پیوسته باشد و تابع
 در
در
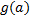 پیوسته باشد .
انگاه تابع مرکب
پیوسته باشد .
انگاه تابع مرکب 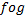 در
در
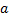 پیوسته است.
پیوسته است.
مثال 6: فرض کنید 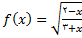 مقادیر برای
مقادیر برای 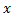 بیابید که به ازای آنها
بیابید که به ازای آنها  پیوسته باشد.
پیوسته باشد.
حل: فرض میکنیم 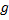 و
و
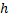 توابعی باشند که به صورت زیر تعریف میشوند
توابعی باشند که به صورت زیر تعریف میشوند
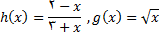 قلمرو
قلمرو 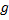 اعداد نامنفی است و قلمرو
اعداد نامنفی است و قلمرو
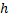 محموعه همه اعداد حقیقی بجز 3- است
محموعه همه اعداد حقیقی بجز 3- است
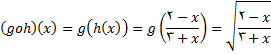
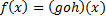
پس میخواهیم قلمرو  را تعیین کنیم قلمرو
را تعیین کنیم قلمرو  مجموعه همه اعدادی است که به ازای انها
مجموعه همه اعدادی است که به ازای انها
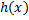 نامنفی باشد یعنی همه اعدادی که به ازای انها داشته باشیم :
نامنفی باشد یعنی همه اعدادی که به ازای انها داشته باشیم :
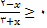 (11)
(11)
برای تعین مقادیری از
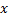 که در (11) صدق میکنند به جدول زیر مراجعه میکنیم. در این جدول بازه هایی را درنظر میگیریم که برای انها
که در (11) صدق میکنند به جدول زیر مراجعه میکنیم. در این جدول بازه هایی را درنظر میگیریم که برای انها
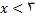 و
و 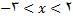 و
و
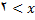 زیرا صورت کسر به ازای
زیرا صورت کسر به ازای
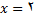 تغیر علامت میدهد. و مخرج کسر به ازای
تغیر علامت میدهد. و مخرج کسر به ازای
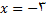 با توجه به این جدول ملاحظه میکنیم که
با توجه به این جدول ملاحظه میکنیم که 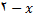 در صورتی وجود دارد که
در صورتی وجود دارد که
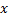 در بازه نیمباز از طرف چپ
در بازه نیمباز از طرف چپ 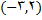 باشد لذا این بازه قلمرو
باشد لذا این بازه قلمرو  است. بنا به قضیه
است. بنا به قضیه
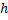 در هر عدد از قلمرو اش پیوسته است یعنی به ازای همه اعداد بجز 3- تابع
در هر عدد از قلمرو اش پیوسته است یعنی به ازای همه اعداد بجز 3- تابع
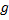 به ازای همه اعداد مثبت پیوسته است. بنابراین از قضیه نتیجه میشود که
به ازای همه اعداد مثبت پیوسته است. بنابراین از قضیه نتیجه میشود که
 در همه مقادیر که پیوسته است و
در همه مقادیر که پیوسته است و
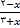 با توجه به جدول فوق این مقادیر اعداد واقع در بازه باز
با توجه به جدول فوق این مقادیر اعداد واقع در بازه باز 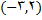 هستند.
هستند.
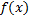 |
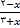 |
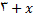 |
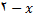 |
|
| وجود ندارد | - | - | + | 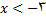 |
| وجود ندارد | نامعین | 0 | 5 | 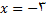 |
| + | + | + | + | 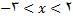 |
| وچود ندارد | - | + | - | 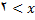 |
در تمرینهای زیر توابع
 و
و
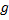 معرفی شده اند در هر تمرین را
معرفی شده اند در هر تمرین را
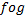 معرفی کنید و همه مقادیر از را بیابید که به ازای آنها پیوسته باشد
معرفی کنید و همه مقادیر از را بیابید که به ازای آنها پیوسته باشد
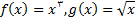
2.
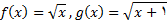
3.
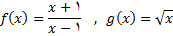
همه مقادیر از 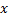 را بیابید که تابع داده شده به ازای انها پیوسته باشد.
را بیابید که تابع داده شده به ازای انها پیوسته باشد.
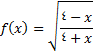
5.
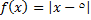
6.
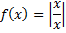
7.
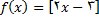
8.