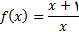ریاضی عمومی / حد بینهایت
تابع
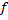 را که با ضابطه
را که با ضابطه
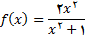 تعریف میشود را در نظر بگیرید
نمودار این تابع در شکل زیر نشان داده شده است.
تعریف میشود را در نظر بگیرید
نمودار این تابع در شکل زیر نشان داده شده است.
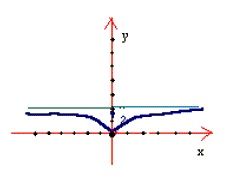
فرض کنید
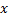 مقادیر 10 و 100 و 1000 و مانند اینها را اختیار کند, و به طور بیکران افزایش یابد. ملاحظه می شود که درحالی که
مقادیر 10 و 100 و 1000 و مانند اینها را اختیار کند, و به طور بیکران افزایش یابد. ملاحظه می شود که درحالی که
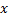 با مقادیر مثبت افزایش پیدا می یابد, مقادیر تابع
با مقادیر مثبت افزایش پیدا می یابد, مقادیر تابع
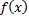 به 2 نزدیک و نزدیکتر می شوند. بخصوص وقتی,
به 2 نزدیک و نزدیکتر می شوند. بخصوص وقتی,
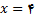 اگر به این کار ادامه دهیم, بطور شهودی ملاحظه میکنیم که مقادیر
اگر به این کار ادامه دهیم, بطور شهودی ملاحظه میکنیم که مقادیر
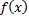 را میتوانیم به دلخواه به 2 نزدیک کنیم به شرطی که
را میتوانیم به دلخواه به 2 نزدیک کنیم به شرطی که
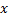 بزرگتر از یک عدد مثبت به اندازه کافی بزرگ, اختیار شود. و یا با یک گام پیشروی برای هر
بزرگتر از یک عدد مثبت به اندازه کافی بزرگ, اختیار شود. و یا با یک گام پیشروی برای هر
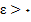 , هرقدر که کوچک باشد, میتوانیم یک عدد
, هرقدر که کوچک باشد, میتوانیم یک عدد
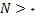 پیدا کنیم که وقتی
پیدا کنیم که وقتی
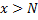 , داشته باشیم
, داشته باشیم
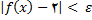 وقتی یک متغیر مستقل مانند x به طور بیکران با مقادیر مثبت افزایش می یابد, مینویسیم
وقتی یک متغیر مستقل مانند x به طور بیکران با مقادیر مثبت افزایش می یابد, مینویسیم
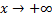 بنابراین, با توجه به مثال توضیحی فوق, میتوان نوشت
بنابراین, با توجه به مثال توضیحی فوق, میتوان نوشت
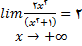
تعریف 1:
فرض کنید f تابعی باشد که به ازای هر عدد در بازه ای مانند
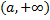 تعریف شده است. می گوئیم حد تابع
تعریف شده است. می گوئیم حد تابع
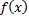 وقتی به طور بیکران افزایش می یابد برابربا عددL است و مینویسیم :
وقتی به طور بیکران افزایش می یابد برابربا عددL است و مینویسیم :
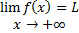 (1)
(1)
اگر برای هر 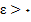 , هر قدر کوچک, یک عدد
, هر قدر کوچک, یک عدد
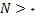 وجود داشته باشد. که وقتی
وجود داشته باشد. که وقتی
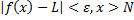 دقت کنید که مقادیر این تابع به ازای اعداد منفی با مقادیر آن به ازای اعداد مثبت متناظر برابر است. پس, به طور شهودی ملاحظه می کنیم که وقتیx به طور بیکران کاهش می یابد,
دقت کنید که مقادیر این تابع به ازای اعداد منفی با مقادیر آن به ازای اعداد مثبت متناظر برابر است. پس, به طور شهودی ملاحظه می کنیم که وقتیx به طور بیکران کاهش می یابد,
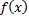 به سمت 2 میل میکند یعنی |f(x)-2|, را میتوان به قدر کافی کوچک اختیار کرد, به این طریق کهx را عددی کوچکتر از یک عدد منفی درنظر بکیریم که قدر مطلق آن به اندازه کافی بزرگ باشد. به طور رسمی می گوییم برای هر ε>0, هرقدر که کوچک باشد, میتوان یک عدد N < 0 یافت که وقتی N>x, داشته باشیم
به سمت 2 میل میکند یعنی |f(x)-2|, را میتوان به قدر کافی کوچک اختیار کرد, به این طریق کهx را عددی کوچکتر از یک عدد منفی درنظر بکیریم که قدر مطلق آن به اندازه کافی بزرگ باشد. به طور رسمی می گوییم برای هر ε>0, هرقدر که کوچک باشد, میتوان یک عدد N < 0 یافت که وقتی N>x, داشته باشیم 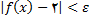 . با استفاده از علامت
. با استفاده از علامت
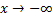 برای نشان دادن این امر که متغیرx به طور بیکران کاهش می یابد مینویسیم
برای نشان دادن این امر که متغیرx به طور بیکران کاهش می یابد مینویسیم
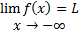 (2)
(2)
اگر برای هر ε>0, هر قدر کوچک , یک عدد
N<0
وجود داشته باشد که وقتی
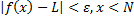
قضیه حدی:
اگر عدد صحیح و مثبتی باشد آنگاه
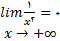 (i)
(i)
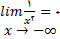 (ii)
(ii)
مثال 1: عبارات زیر را محاسبه کنید
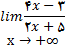
حل: برای استفاده از قضیه حدی, صورت و مخرج کسر را برx تقسیم میکنیم و به دست می اوریم
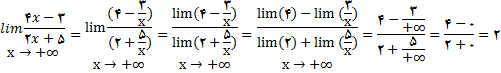
مثال 2: عبارات زیر را محاسبه کنید
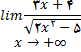
حل: صورت و مخرج کسر را برx تقسیم میکنیم. در مخرج فرض میکنیم
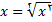 زیرا تنها مقادیر مثبت x مورد نظر ما هستند
زیرا تنها مقادیر مثبت x مورد نظر ما هستند
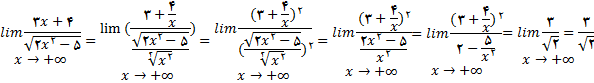
مثال 3: عبارت زیر را محاسبه نمائید
حل:
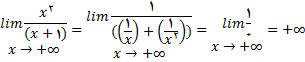
بنابراین, حد مخرج صفر است . مخرج با مقادیر مثبت به سمت صفر میل میکند حد صورت برابر 1 است و لذا بنا به قضیه حدی 12 (i) نتیجه می شود که
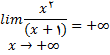
تعریف
گفته میشود خط y=b یک مجانب افقی نمودار تابع f است اگر دست کم یکی از عبارات زیر درست باشد .
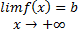 و به ازای یک عدد
و به ازای یک عدد
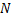 وقتی
وقتی
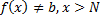
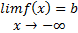 و به ازای یک عدد
و به ازای یک عدد
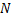 وقتی
وقتی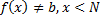
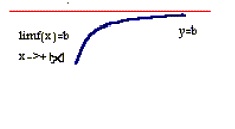
نمونه 1: در هریک از شکلهای زیر قسمتی از نمودار تابعی نشان داده شده است که خط y=b برای آن یک مجانب افقی است
 |
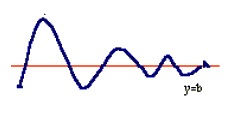 |
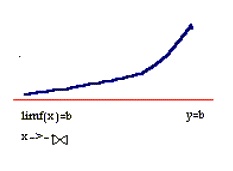 |
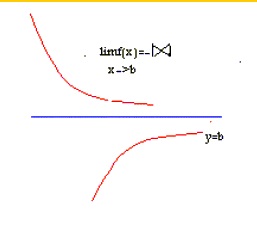 |
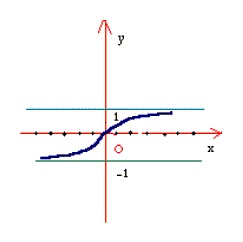
مثال 4 : مجانبهای افقی نمودار تابع
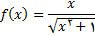 را بیابید و نمودارش را رسم کنید
را بیابید و نمودارش را رسم کنید
حل :
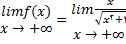
برای محاسبه این حد مینویسیم
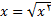 و
و
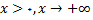 صورت و مخرج را بر
صورت و مخرج را بر
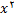 تقسیم میکنیم
تقسیم میکنیم
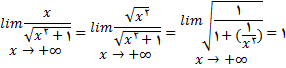
پس بنا به تعریف(i) خط y=1یک مجانب افقی است اکنون
 را در نظر بگیریم
در این حالت مینویسیم
را در نظر بگیریم
در این حالت مینویسیم  زیرا اگر
زیرا اگر
 صورت و مخرج با استفاده از
صورت و مخرج با استفاده از 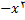 تبدیل میکنیم
لذا
تبدیل میکنیم
لذا
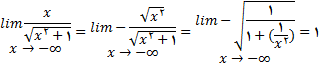
پس بنا به تعریف (ii) خط y=1 یک مجانب افقی است. نمودار در شکل زیر رسم شده است
مثال 5: مجانبهای افقی و قائم نمودار تابع
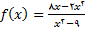 نمودار تابع را رسم کنید
نمودار تابع را رسم کنید
حل:
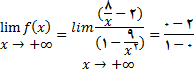
بنا بر این
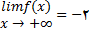 (1)
(1)
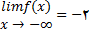 (2)
(2)
اگر در صورت و مخرج کسر را تجزیه کنیم داریم
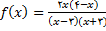
چهار حد زیر را درنظر بگیریم
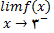
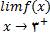
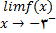
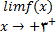
برای محاسبه
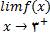
ملاحظه کنید که
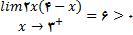
و
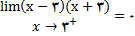
که در آن (x-3)(x+3) با مقادیر مثبت به سمت صقر میل میکند لذا بنا به قضیه حدی 12 (i) داریم
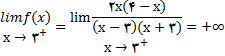
چون
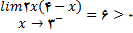
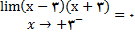
که در آن (x-3)(x+3) با مقادیر منفی به سمت صفر میل میکند, از قضیه حدی
12 (ii) نتیجه می شود که
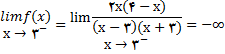
با استفاده از قضیه حدی 12 (iv) , f(x) را محاسبه میکنیم
چون
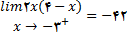
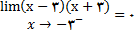
که در آن (x-3)(x+3) با مقادیر منفی به سمت صفر میل میکند, پس
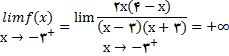 (5)
(5)
چون
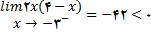
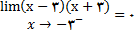
که در آن (x-3)(x+3) با مقادیر مثبت به سمت صفر میل میکند, با توجه به قضیه حدی 12 (iii) داریم
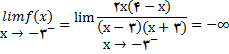 (6)
(6)
از (1) و (2) و تعریف این نتیحه به دست می آید که خط
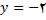 یک مجانب افقی نمودارf است. (3) تا (6) و تعریف نتیجه می شود که خطوط
یک مجانب افقی نمودارf است. (3) تا (6) و تعریف نتیجه می شود که خطوط
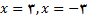 مجانبهای قائم نمودار هستند . با توجه به معادله داده شده, نمودار f شامل نقاط (5,5) و (4,5) است معدودی از نقاط دیگر را مشخص میکنیم و از اطلاعاتی که در (1) و (6) نهفته است بهره میگیریم تا نمودار مربوطه را ایجاد کنیم.
مجانبهای قائم نمودار هستند . با توجه به معادله داده شده, نمودار f شامل نقاط (5,5) و (4,5) است معدودی از نقاط دیگر را مشخص میکنیم و از اطلاعاتی که در (1) و (6) نهفته است بهره میگیریم تا نمودار مربوطه را ایجاد کنیم.
مثال6: با استفاده از تعریف ثابت کنید.
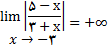
حل: به ازای هر N>0 باید δ>0 را طوری تعین کنیم که داشته باشیم
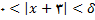 وقتی که
وقتی که
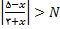 و یا
(1)
و یا
(1) 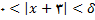 وقتی که
وقتی که
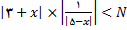 حال با انتخاب
حال با انتخاب
 مناسب یک کران بالا برای
مناسب یک کران بالا برای
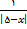 تعین میکیم اگر
تعین میکیم اگر 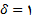 اختیار شود
میتوان نوشت
اختیار شود
میتوان نوشت
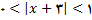 و یا به عبارت دیگر
و یا به عبارت دیگر
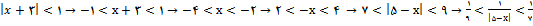
با استفاده از 1 و 2 داریم
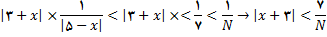
و با استفاده از 3 و
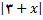 کافی است که
کافی است که
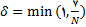 اختیار شود
اختیار شود
مثال7: حد تابع
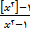 وقتی x به سمت 1 میل میکند را بیابید.
وقتی x به سمت 1 میل میکند را بیابید.
حل: چون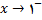 داریم
داریم
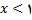 اگر
اگر
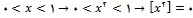 بنابراین
بنابراین
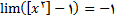 و
و
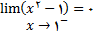 و چون
و چون
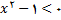 پس مخرج با مقادیر منفی
پس مخرج با مقادیر منفی
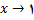 به سمت صفر میل میکند و در نتیجه
به سمت صفر میل میکند و در نتیجه
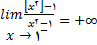
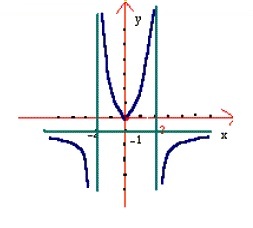
مثال 8: مجانبهای تابع 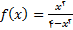 را بیابید
را بیابید
حل: چون با تبدیل
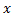 به
به
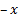 معادله عوض نمی شود پس نمودار تابع نسبت به محور
معادله عوض نمی شود پس نمودار تابع نسبت به محور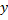 ها متقارن است. ابتدا نمودار تابع را برای
ها متقارن است. ابتدا نمودار تابع را برای
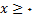 رسم کرده و سپس با استفاده از خاصیت تقارن شکل را کامل میکنیم
رسم کرده و سپس با استفاده از خاصیت تقارن شکل را کامل میکنیم
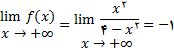
در نتیجه 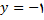 مجانب افقی تابع می باشد . چون
مجانب افقی تابع می باشد . چون
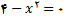 اگر
اگر 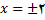 باشد . بنابراین خط
باشد . بنابراین خط
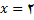 ممکن است مجانب قائم تابع باشد و چون
ممکن است مجانب قائم تابع باشد و چون
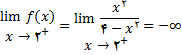
پس خط
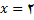 مجانب قائم بوده و منحنی نمودار تابع از سمت راست به این مجانب میل خواهد کرد. از طرف دیگر چون
مجانب قائم بوده و منحنی نمودار تابع از سمت راست به این مجانب میل خواهد کرد. از طرف دیگر چون
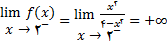
نتیجه میدهد که منحنی نمودار تابع از سمت چپ به این مجانب میل خواهد کرد. و چون
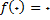 لذا منحنی از مبدا نیز میگذرد.
لذا منحنی از مبدا نیز میگذرد.
در تمرینهای زیر حد های خواسته شده
را محاسبه کنید .
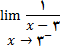
2.
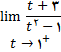
3.
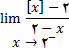
4.
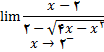
5.
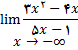
6.
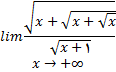
مجانبهای قائم و افقی معادله های زیر را بنویسید.
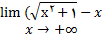
8.
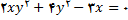
9.
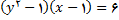
10.
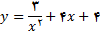
11.