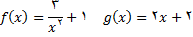مشتق / مشتق توابع مرکب
تصور کنید که
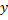 تابعی از
تابعی از
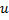 و
و
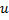 به نوبه خود تابعی از
به نوبه خود تابعی از
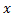 باشد. مثلا فرض کنید
باشد. مثلا فرض کنید
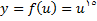 (1)
(1)
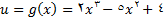 (2)
(2)
معادلات (1) و (2) , همراه با هم
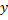 را به عنوان تابعی از
را به عنوان تابعی از
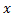 تعریف میکنند زیرا اگر در معادله (1) به جای
تعریف میکنند زیرا اگر در معادله (1) به جای
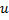 , طرف راست معادله (2) را قرار دهیم, داریم
, طرف راست معادله (2) را قرار دهیم, داریم
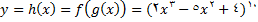
که در آن
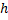 تابع مرکبی است که قبلا تعریف شده است.
یک قضیه مهم در مورد مشتق گیری از توابع مرکب در زیر امده است که به نام قاعده زنجیره ای معروف است.
تابع مرکبی است که قبلا تعریف شده است.
یک قضیه مهم در مورد مشتق گیری از توابع مرکب در زیر امده است که به نام قاعده زنجیره ای معروف است.
قضیه 1-7: ( قاعده زنجیره ای)
فرض کنید
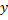 تابعی از
تابعی از
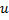 است که به صورت
است که به صورت
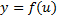 تعریف شده است, و
تعریف شده است, و
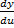 وجود دارد, و نیز فرض کنید
وجود دارد, و نیز فرض کنید
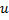 تابعی از
تابعی از
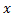 است که به صورت
است که به صورت
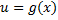 تعریف شده است, و
تعریف شده است, و
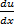 وجود دارد, در اینصورت,
وجود دارد, در اینصورت,
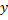 تابعی از
تابعی از
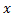 است و
است و
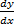 وجود دارد و از رابطه زیر به دست می آید.
وجود دارد و از رابطه زیر به دست می آید.
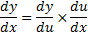
قبل از اثبات قاعده زنجیره ای, نمونه ای ارائه میدهیم که کارکرد این را نشان میدهد.
نمونه 1: 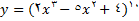 برای به دست امدن
برای به دست امدن
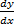 ,
,
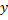 را تابعی از
را تابعی از
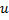 درنظر میگیریم که
درنظر میگیریم که
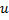 تابعی از
تابعی از
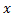 است. پس
است. پس
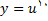 که در آن
که در آن
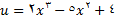 بنابراین, با استفاده از قاعده زنجیره ای خواهید داشت
بنابراین, با استفاده از قاعده زنجیره ای خواهید داشت
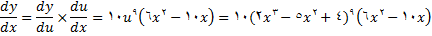
نمونه 2: مشتق تابع نمونه 1 ا با استفاده از قاعده زنجیری و نماد تابع مرکب محاسبه میکنیم.
اگر
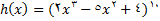 فرض کنید
فرض کنید
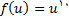 و
و
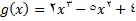 و انگاه
و انگاه
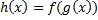 بنابراین
بنابراین
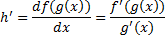
چون
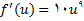 پس
پس
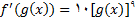 و
و
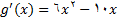 لذا
لذا
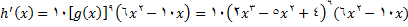
مثال1 : فرض کنید
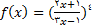 ,
,
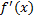 را پیدا کنید.
را پیدا کنید.
حال با استفاده از قاعده زنجیری داریم
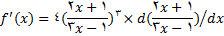
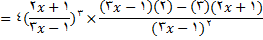
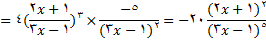
در تمرینهای زیر, مشتق تابع داده شده را حساب کنید
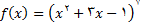
2.
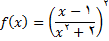
3.
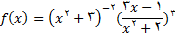
در تمرینهای زیر مشتق تابع
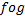 را حساب کنید.
را حساب کنید.
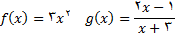
5.