معادلات دیفرانسیل / اشنائی با معادلات دیفرانسیل و مفاهیم اولیه
يك سري تواني ازx بصورت
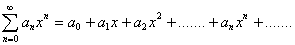 مي باشد.
مي باشد.
تعريف معادله خطي همگن مرتبه دوم به صورت
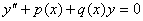 را در نظر بگيريد.
نقطه
x0
را نقطه عادي مي گوييم اگر هردو تابع p و q در x0 تحليلي باشد ( سري در x0
همگرا باشد ).اگر حد اقل يكي از p و q ها تحليلي نباشد انگاه x0 را نقطه تكين مي ناميم .
به عبارت ديگر اگر درحالتي كه p و q كسري هستند در نقطه اي كه مخرج كسر صفر نشود تحليلي هستند و نقاطي كه مخرج صفر مي شود تكين هستند.
را در نظر بگيريد.
نقطه
x0
را نقطه عادي مي گوييم اگر هردو تابع p و q در x0 تحليلي باشد ( سري در x0
همگرا باشد ).اگر حد اقل يكي از p و q ها تحليلي نباشد انگاه x0 را نقطه تكين مي ناميم .
به عبارت ديگر اگر درحالتي كه p و q كسري هستند در نقطه اي كه مخرج كسر صفر نشود تحليلي هستند و نقاطي كه مخرج صفر مي شود تكين هستند.
مثال : جواب معادله ديفرانسيل 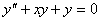 را در مجاورت نقطه x0 به صورت سري تواني بنويسيد.
را در مجاورت نقطه x0 به صورت سري تواني بنويسيد.
حل : در اين مسئله p(x)=x و q(x)=1 بنابر اين جواب معادله بصورت زیر خواهد بود.
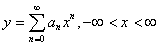
در نتيجه اگر معادلات
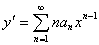
و
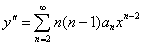
را در معادله ديفرانسيل اصلی قرار مي دهيم خواهيم داشت .
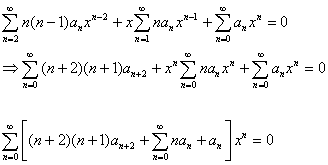
از اين جا نتيجه ميشود كه همه ضرايب سري بايد صفر باشد يعني
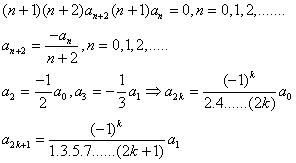
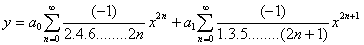
مثال : معادله ديفرانسيل
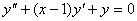 را حل كنيد
و x را طوري به دست آوريد كه در روابط
را حل كنيد
و x را طوري به دست آوريد كه در روابط
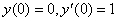 صدق کند.
صدق کند.
پاسخ
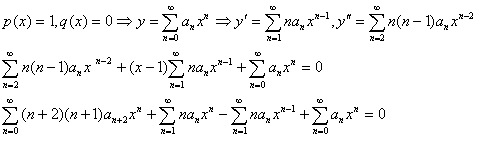
يا
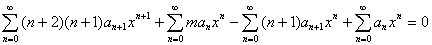
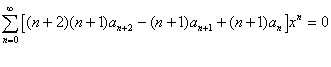
از اين جا نتيجه مي شود:
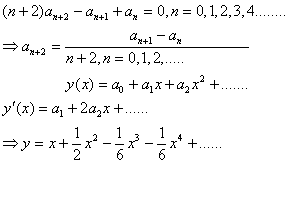
مثال :معادله ديفرانسيل
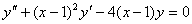 را در مجاورت x0 = 1 حل كنيد .
را در مجاورت x0 = 1 حل كنيد .
حل : جواب بصورت يك سري تواني از x-1 مي باشد .يعني
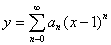
در نتيجه
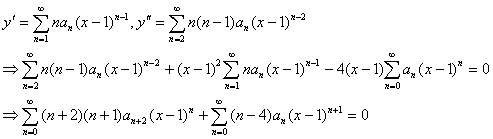
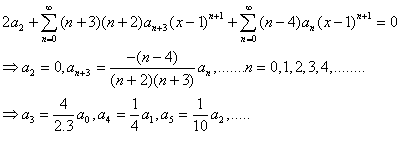
و براي k>=2 داريم :
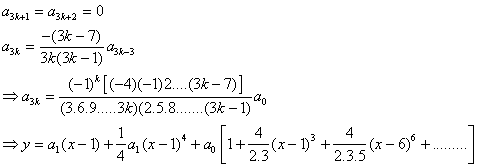
تعريف :
نقطه x0 را يك نقطه تكين منظم معادله
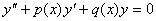 مي ناميم هرگاه x0
يك نقطه تكين معادله بوده و تابع
مي ناميم هرگاه x0
يك نقطه تكين معادله بوده و تابع
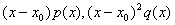 در x0 تحليلي باشد.
اگر حد اقل يكي از دو تابع در x0 تحليلي نباشد آنگاه x0 را يك نقطه تكين نامنظم ناميده مي شود .
در x0 تحليلي باشد.
اگر حد اقل يكي از دو تابع در x0 تحليلي نباشد آنگاه x0 را يك نقطه تكين نامنظم ناميده مي شود .
حل يك دستگاه معادله ديفرانسيل :
قبلا با دستگاههای معادلات دیفرانسیل اشنا شده اید حال به حل چند مثال از این نوع خواهیم پرداخت
مثال :دستگاه زیر را حل كنيد :
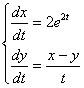
حل :
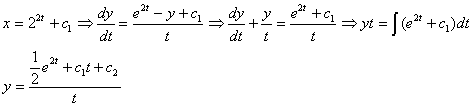
مثال : دستگاه زير را حل كنيد :
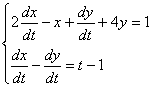
حل :
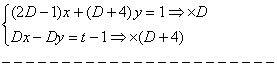
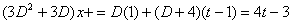
وحل اين معادله ديفرانسيل عبارت است از
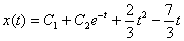
كه اگر در معادله قبلي جايگزين كنيم خواهيم داشت.
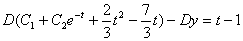
حال انتگرال مي گيريم
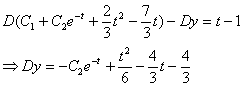
با جا گذاري در معادله اول داريم :
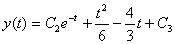
بعد از عمل كردن D
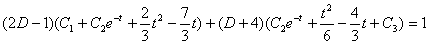
تمرين: دستگاه معادلات ديفرانسيل زير را حل كنيد .
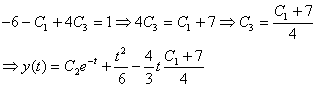
2.