مشتق / مشتق توابع نمائی
اگر
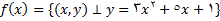
, آنگاه معادله
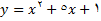 (1)
(1)
تابع
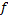 را به طور صریح تعریف میکند. ولی هر تابعی را نمی توان به طور صریح تعریف کرد. به عنوان مثال, در معادله
را به طور صریح تعریف میکند. ولی هر تابعی را نمی توان به طور صریح تعریف کرد. به عنوان مثال, در معادله
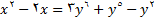 (2)
(2)
نمی توانیم
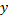 را بر حسب
را بر حسب
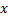 به دست آوریم, با وجود این ممکن است یک یا چند تابع
به دست آوریم, با وجود این ممکن است یک یا چند تابع
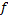 به صورت
به صورت
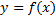 وجود داشته باشند که در معادله (2) صدق کنند. یعنی معادله
وجود داشته باشند که در معادله (2) صدق کنند. یعنی معادله
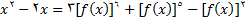
برای تمام مقادیر
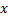 واقع در قلمرو
واقع در قلمرو
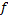 برقرار باشد. در این حالت, معادله (2) تابع را به طور ضمنی تعریف میکند.
برقرار باشد. در این حالت, معادله (2) تابع را به طور ضمنی تعریف میکند.
با فرض اینکه معادله (2),
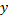 را به عنوان حداقل یک تابع مشتق پذیر از
را به عنوان حداقل یک تابع مشتق پذیر از
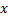 تعریف می کند, میتوانیم مشتق
تعریف می کند, میتوانیم مشتق
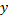 نسبت به
نسبت به
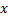 را با فرایندی موسوم به مشتق گیری ضمنی پیدا کنیم, که اکنون این کار را میکنیم. طرف چپ معادله (2) تابعی از
را با فرایندی موسوم به مشتق گیری ضمنی پیدا کنیم, که اکنون این کار را میکنیم. طرف چپ معادله (2) تابعی از
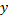 و طرف راست آن تابعی از
و طرف راست آن تابعی از
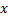 است.
است.
فرض کنید
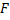 تابعی باشدکه به وسیله طرف چپ معادله (2) تعریف میشود. و
تابعی باشدکه به وسیله طرف چپ معادله (2) تعریف میشود. و
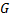 تابعی باشد که به وسیله طرف راست آن تعریف می شود. بدین ترتیب داریم
تابعی باشد که به وسیله طرف راست آن تعریف می شود. بدین ترتیب داریم
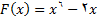 (3)
(3)
که در آن
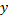 تابعی از
تابعی از
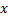 , مثلا به صورت
, مثلا به صورت
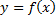 است
بنابراین, معادله (2) را به صورت زیر میتوان نوشت.
است
بنابراین, معادله (2) را به صورت زیر میتوان نوشت.
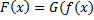 (5)
(5)
معادله (5) به ازای تمام مقادیر
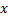 واقع در قلمرو
واقع در قلمرو
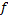 که برای آنها وجود داشته باشد, برقرار است. در اینصورت برای تمام مقادیر
که برای آنها وجود داشته باشد, برقرار است. در اینصورت برای تمام مقادیر
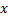 که به ازای آنها تابع
که به ازای آنها تابع
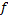 که برای آنها
که برای آنها
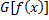
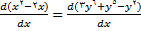 (6)
(6)
مشتق طرف چپ معادله (6) را به آسانی میتوان پیدا کرد.
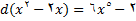 (7)
(7)
با استفاده از قاعده زنجیری, مشتق طرف راست معادله (6) را پیدا میکنیم
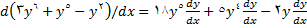 (8)
(8)
اگر مقادیر مربوطه را از (7) و (8) در معادله (6) قرار دهیم, داریم
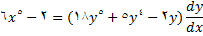
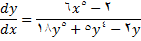
معادله (2) نوع ویژه ای از معادله شامل 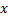 و
و
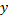 است زیرا میتوان آن را طوری نوشت که تمام جملات شامل
است زیرا میتوان آن را طوری نوشت که تمام جملات شامل
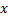 در طرف چپ و تمام جملات شامل
در طرف چپ و تمام جملات شامل
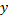 در طرف راست معادله قرار داشته باشند. در نمونه زیر, روش مشتق گیری ضمنی را برای محاسبه
در طرف راست معادله قرار داشته باشند. در نمونه زیر, روش مشتق گیری ضمنی را برای محاسبه
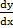 از یک نوع معادله کلی تر به کار می بریم.
از یک نوع معادله کلی تر به کار می بریم.
نمونه 1: معادله زیر را درنظر بگیرید.
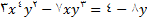 (9)
(9)
و فرض کنید حداقل یک تابع مشتق پذیر
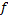 به صورت
به صورت
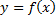 وجود دارد که در معادله (9) صدق میکند. اگر از دو طرف معادله (9) مشتق بگیریم (و به خاطر داشته باشیم که
وجود دارد که در معادله (9) صدق میکند. اگر از دو طرف معادله (9) مشتق بگیریم (و به خاطر داشته باشیم که
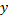 تابع مشتق پذیری از
تابع مشتق پذیری از
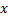 است) با استفاده از قضایای مربوط به مشتق حاصلضرب, مشتق تابع توانی و قاعده زنجیره ای به دست می آوریم
است) با استفاده از قضایای مربوط به مشتق حاصلضرب, مشتق تابع توانی و قاعده زنجیره ای به دست می آوریم
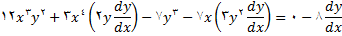
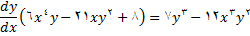
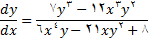
این را به خاطر داشته باشیم که فرض کرده بودیم, هر دو معادله (2) و (9),
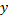 را به صورت حداقل یک تابع مشتق پذیر از
را به صورت حداقل یک تابع مشتق پذیر از
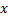 تعریف میکنند. ممکن است یک معادله شامل
تعریف میکنند. ممکن است یک معادله شامل
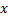 و
و
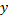 , وجود هیچ تابع حقیقی را ایجاب نکند, همانطور که معادله زیرایجاب نمی کند.
, وجود هیچ تابع حقیقی را ایجاب نکند, همانطور که معادله زیرایجاب نمی کند.
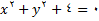
معادله فوق به ازای هیچ مقدار حقیقی از
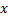 و
و
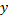 برقرار نیست. بعلاوه ممکن است در معادله ای از
برقرار نیست. بعلاوه ممکن است در معادله ای از
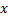 و
و
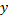 توابع مختلفی صدق کنند که بعضی از آنها مشتق پذیر باشند و بعضی نباشند.
بحث کلی در این مورد خارج از توان ولی در کتابهای حساب دیفرانسیل و انتگرال پیشرفته دیده می شود. در بحث های بعدی, وقتی می گوییم که یک معادله از
توابع مختلفی صدق کنند که بعضی از آنها مشتق پذیر باشند و بعضی نباشند.
بحث کلی در این مورد خارج از توان ولی در کتابهای حساب دیفرانسیل و انتگرال پیشرفته دیده می شود. در بحث های بعدی, وقتی می گوییم که یک معادله از
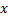 و
و
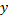 ,
,
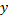 را به طور ضمنی به عنوان تابعی از
را به طور ضمنی به عنوان تابعی از
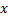 تعریف میکند, فرض بر این است که یک یا چند تا از این توابع مشتق پذیرند. مثال زیر که به دنبال می آید, این واقعیت را نشان می دهد که مشتق گیری ضمنی, مشتق دو تابع مشتق پذیر را که به وسیله معادله مفروض تعریف شده اند, به دست میدهد.
تعریف میکند, فرض بر این است که یک یا چند تا از این توابع مشتق پذیرند. مثال زیر که به دنبال می آید, این واقعیت را نشان می دهد که مشتق گیری ضمنی, مشتق دو تابع مشتق پذیر را که به وسیله معادله مفروض تعریف شده اند, به دست میدهد.
مثال1: معادله ای به صورت
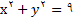 داده شده است
داده شده است
الف) 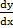 را به وسیله مشتق گیری ضمنی پیدا کنید
را به وسیله مشتق گیری ضمنی پیدا کنید
ب) دو تابع پیدا کنید که به وسیله معادله فوق تعریف شوند
پ) از راه مشتق گیری صریح, مشتق توابع یافته شده در قسمت (ب) رابیابید.
ت) تحقیق کنید که تابع قسمت (الف) و قسمت (ب) با هم مطابقت دارند.
حل:
(الف) از مشتق گیری ضمنی به دست می اوریم
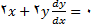
و بنا براین
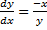
(ب) معادله داده شده را نسبت به
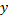 حل میکنیم و به دست می آوریم
حل میکنیم و به دست می آوریم
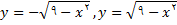
فرض کنید
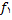 و
و
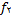 به صورت زیر تعریف شوند
به صورت زیر تعریف شوند
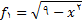
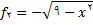
(پ) چون
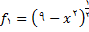 , با استفاده از قاعده زنجیره ای داریم
, با استفاده از قاعده زنجیره ای داریم
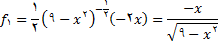
به طریق مشابه
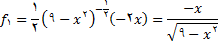
(ت) برای
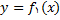 که به صورت
که به صورت
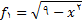 تعریف شده است, از قسمت (پ) داریم
تعریف شده است, از قسمت (پ) داریم
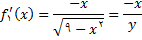
که با جواب قسمت (الف) مطابقت دارد.
برای
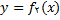 که به صورت
که به صورت
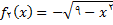 تعریف میشود, از قسمت (ب) داریم
تعریف میشود, از قسمت (ب) داریم
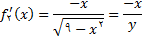
که باز هم با نتیجه قسمت (الف) مطابقت دارد.
در تمرین های زیر با استفاده از مشتق گیری ضمنی را پیدا کنید.
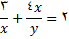
2.
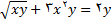
3.
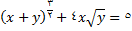
4.