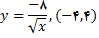مشتق / خط مماس
بسیاری از مسائل مهم حساب دیفرانسیل و انتگرال, به مساله پیدا کردن خط مماس وارد بر منحنی در یک نقطه معین روی منحنی مربوط می شوند. در هندسه مسطحه اگر منحنی دایره باشد, خط مماس در یک نقطه
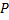 روی دایره, به عنوان خطی تعریف میشود
که دایره را فقط در یک نقطه قطع میکند. این تعریف در حالت کلی برای همه منحنی ها صادق نیست. به عنوان مثال در شکل زیر خطی که میخواهیم در نقطه
روی دایره, به عنوان خطی تعریف میشود
که دایره را فقط در یک نقطه قطع میکند. این تعریف در حالت کلی برای همه منحنی ها صادق نیست. به عنوان مثال در شکل زیر خطی که میخواهیم در نقطه
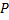 بر منحنی مماس باشد, منحنی را در نقطه دیگری مانند
بر منحنی مماس باشد, منحنی را در نقطه دیگری مانند
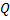 قطع خواهد کرد.
قطع خواهد کرد.
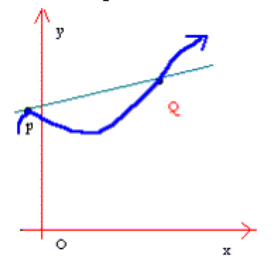
در این بخش, تعریف مناسبی از خط مماس بر نمودار یک تابع در نقطه ای روی نمودار ارائه میدهیم. برای این کار, ضریب زاویه خط مماس در یک نقطه را تعریف میکنیم, زیرا اگر ضریب زاویه یک خط و نقطه ای
روی آن معلوم باشد, آن خط معین میشود. تصور کنید تابع
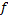 در
در
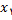 پیوسته است. میخواهیم ضریب زاویه خط مماس بر نمودار
پیوسته است. میخواهیم ضریب زاویه خط مماس بر نمودار
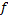 در نقطه
در نقطه
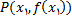 را به دست آوریم. فرض کنید
را به دست آوریم. فرض کنید
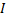 بازه بازی باشد که شامل
بازه بازی باشد که شامل
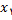 است و
است و
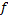 بر این بازه تعریف شده است. نقطه دیگر
بر این بازه تعریف شده است. نقطه دیگر
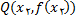 را روی نمودار
را روی نمودار
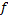 در نظر می گیریم به طوری که
در نظر می گیریم به طوری که
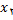 نیز در
نیز در
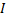 باشند خطی را که از
باشند خطی را که از
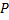 و
و
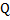 می گذرد رسم میکنیم. هرخطی که از دو نقطه یک منحنی بگذرد, خط قاطع نامیده می شود, پس خط گذرنده از
می گذرد رسم میکنیم. هرخطی که از دو نقطه یک منحنی بگذرد, خط قاطع نامیده می شود, پس خط گذرنده از
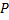 و
و
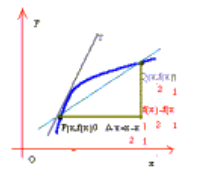
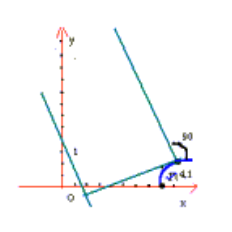
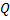 یک خط قاطع است. در شکل زیر خط قاطع به ازای مقادیر مختلف
یک خط قاطع است. در شکل زیر خط قاطع به ازای مقادیر مختلف
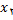 رسم شده است. در شکل دیگر یک خط قاطع خاص نشان داده شده است. در این شکل
رسم شده است. در شکل دیگر یک خط قاطع خاص نشان داده شده است. در این شکل
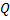 در طرف راست
در طرف راست
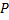 قرار دارد. معهذا,
قرار دارد. معهذا,
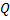 می تواند در طرف چپ
می تواند در طرف چپ
 نیز باشد, همچنانکه در شکل زیر دیده میشود.
نیز باشد, همچنانکه در شکل زیر دیده میشود.
تفاضل طولهای نقاط
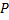 و
و
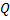 را با
را با
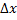 نشان میدهیم. بنابراین
نشان میدهیم. بنابراین
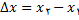 ممکن است مثبت یا منفی باشد. پس ضریب زاویه خط قاطع
ممکن است مثبت یا منفی باشد. پس ضریب زاویه خط قاطع
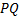 به شرطی که
به شرطی که
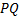 قائم نباشد, از رابطه زیر به دست میآید.
قائم نباشد, از رابطه زیر به دست میآید.
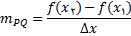
چون
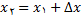 معادله فوق را میتوانیم به صورت زیربنویسیم
معادله فوق را میتوانیم به صورت زیربنویسیم
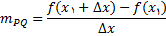
حال فرض کنید نقطه ثابت
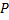 باشد, و نقطه
باشد, و نقطه
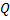 در طول منحنی به طرف
در طول منحنی به طرف
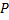 حرکت دهیم, یعنی
حرکت دهیم, یعنی
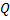 به سمت
به سمت
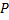 میل کند. این عمل معادل است با اینکه
میل کند. این عمل معادل است با اینکه
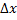 را به سمت صفر میل بدهیم. ضمن انجام این عمل, خط قاطع حول نقطه ثابت
را به سمت صفر میل بدهیم. ضمن انجام این عمل, خط قاطع حول نقطه ثابت
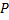 گردش میکند. اگر این خط قاطع دارای یک وضعیت حدی باشد, همین وضعیت حدی است که ما میخواهیم خط مماس بر نمودار در نقطه
گردش میکند. اگر این خط قاطع دارای یک وضعیت حدی باشد, همین وضعیت حدی است که ما میخواهیم خط مماس بر نمودار در نقطه
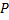 باشد. از اینرو میخواهیم ضریب زاویه خط مماس بر نمودار
باشد. از اینرو میخواهیم ضریب زاویه خط مماس بر نمودار
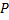 در برابر با حد
در برابر با حد
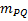 باشد وقتی که
باشد وقتی که
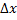 به سمت صفر میل میکند, البته چنانچه این حد وجود داشته باشد. اگر
به سمت صفر میل میکند, البته چنانچه این حد وجود داشته باشد. اگر
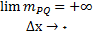 یا
یا
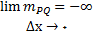 , آنگاه
, آنگاه
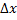 به صفر میل میکند و خط
به صفر میل میکند و خط
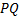 به سمت خطی که از
به سمت خطی که از
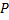 میگذرد و موازی محور
میگذرد و موازی محور
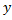 هاست میل میکند. در این حالت میخواهیم خط مماس بر منحنی در
هاست میل میکند. در این حالت میخواهیم خط مماس بر منحنی در
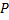 همان خط
همان خط
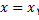 باشد از بحث فوق به نتیجه زیر میرسیم.
باشد از بحث فوق به نتیجه زیر میرسیم.
تعریف 1 : فرض کنید تابع
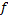 در
در
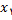 پیوسته باشد. خط مماس بر نمودار ب در نقطه
پیوسته باشد. خط مماس بر نمودار ب در نقطه
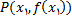 عبارت است از (i) خطی که از
عبارت است از (i) خطی که از 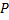 میگذرد و دارای ضریب زاویه
میگذرد و دارای ضریب زاویه
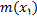 است که از رابطه زیر بدست می آید
است که از رابطه زیر بدست می آید
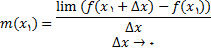 (i)
(i)
به شرطی که این حد وجود داشته باشد.
(ii) خط
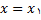 اگر
اگر
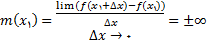
اگر هیچکدام از حالات (i) و (ii) تعریف برقرار نباشد, آنگاه خط مماس برنمودار در نقطه
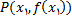 وجود ندارد.
وجود ندارد.
مثال 1: سهمی
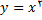 مفروض است. در هریک از قسمتهای (الف) تا (پ) ضریب زاویه خط قاطعی را که از دو نقطه داده شده میگذرد, بیابید.
مفروض است. در هریک از قسمتهای (الف) تا (پ) ضریب زاویه خط قاطعی را که از دو نقطه داده شده میگذرد, بیابید.
الف) 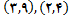
ب) 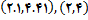
پ) 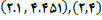
ت) ضریب زاویه خط مماس بر سهمی را در نقطه
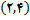 را بدست آورید.
را بدست آورید.
حل: حل فرض کنید
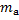 ,
,
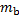 و
و
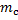 , به ترتیب ضریب زاویه خطوط قاطع در قسمتهای (الف), (ب) و(پ) باشند.
, به ترتیب ضریب زاویه خطوط قاطع در قسمتهای (الف), (ب) و(پ) باشند.
الف) 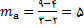
ب) 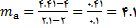
پ) 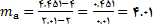
ت) 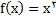 با استفاده از 1 داریم:
با استفاده از 1 داریم:
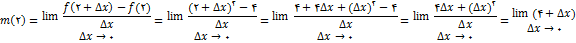
تعریف 2 : خط قائم بر منحنی در نقطه ای مفروض, عبارت است از خط عمود بر خط مماس در ان نقطه
مثال: معادله آن خط قائم بر منحنی
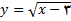 را که موازی خط
را که موازی خط
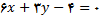 باشد, را پیدا کنید.
باشد, را پیدا کنید.
حل: فرض کنید
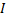 خط مفروض باشد. برای یافتن ضریب زاویه
خط مفروض باشد. برای یافتن ضریب زاویه
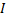 , معادله آن را به صورت ضریب زاویه – عرض از مبدا, مینویسیم
, معادله آن را به صورت ضریب زاویه – عرض از مبدا, مینویسیم
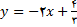 پس ضریب زاویه برابر با
پس ضریب زاویه برابر با
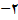 است و ضریب زاویه خط قائم مطلوب نیز
است و ضریب زاویه خط قائم مطلوب نیز
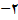 است زیرا دو خط با هم موازیند . برای یافتن ضریب زاویه خط مماس بر منحنی داده شده در نقطه
است زیرا دو خط با هم موازیند . برای یافتن ضریب زاویه خط مماس بر منحنی داده شده در نقطه
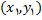 , تعریف را با ضابطه
, تعریف را با ضابطه
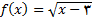 به کار میبریم .
به کار میبریم .
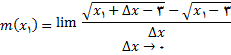
برای محاسبه حد فوق, صورت را گویا میکنیم
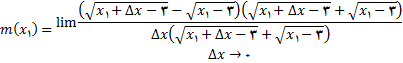
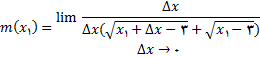
اگر صورت و مخرج را بر
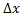 تقسیم کنیم (چون
تقسیم کنیم (چون
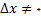 ) , به دست می آوریم
) , به دست می آوریم
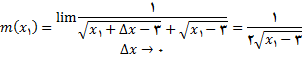
چون خط قائم در یک نقطه عمود بر خط مماس در آن نقطه است, حاصلضرب ضریب زاویه های آنها برابر
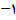 است. بنابر این , ضریب زاویه خط قائم در
است. بنابر این , ضریب زاویه خط قائم در
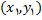 از رابطه زیر به دست می آید.
از رابطه زیر به دست می آید.
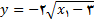
همچنانکه در بالا نشان داده شد, ضریب زاویه خط مطلوب برابر با
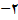 است. بنابراین, معادله
است. بنابراین, معادله
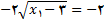 را حل میکنیم تا به دست بیاید
را حل میکنیم تا به دست بیاید
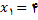 پس , خط مطلوب از نقطه
پس , خط مطلوب از نقطه
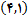 روی منحنی میگذرد و ضریب زاویه آن
روی منحنی میگذرد و ضریب زاویه آن
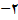 است . معادله چنین خطی به صورت نقطه- ضریب زاویه ای عبارت است از
است . معادله چنین خطی به صورت نقطه- ضریب زاویه ای عبارت است از
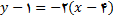 و یا
و یا
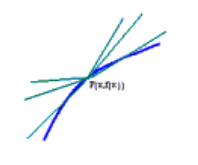
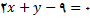 . به شکل زیر مراجعه کنید, که نمودار منحنی را همراه با خط, خط قائم در نقطه
. به شکل زیر مراجعه کنید, که نمودار منحنی را همراه با خط, خط قائم در نقطه
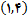 و خط مماس
و خط مماس
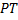 در نقطه
در نقطه
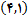 را نشان میدهد.
را نشان میدهد.
در تمرینهای 1 تا 6 , ضریب زاویه خط مماس بر منحنی در نقطه
 را به دست اورید. جدولی از مقادیر
را به دست اورید. جدولی از مقادیر
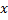 ,
,
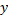 و
و
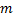 روی بازه بسته
روی بازه بسته
![[a,b]](document/mathEdu_011_files/image069.png) بنویسید و دقت کنید تمام نقاطی که در آنها نمودار دارای خط مماس افقی است, در این جدول باشند. نمودار را نیز رسم کنید , و قطعه ای از خط مماس را در هریک از نقاط رسم شده نشان دهید
بنویسید و دقت کنید تمام نقاطی که در آنها نمودار دارای خط مماس افقی است, در این جدول باشند. نمودار را نیز رسم کنید , و قطعه ای از خط مماس را در هریک از نقاط رسم شده نشان دهید
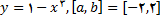
2.
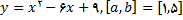
در تمرینهای زیر, ضریب زاویه خط مماس بر نمودار در نقطه
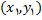 را به دست اورید. جدولی از مقادیر
را به دست اورید. جدولی از مقادیر
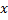 ,
,
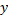 و
و
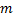 در نقاط مختلف روی نمودار بنویسید و دقت کنید تمام نقاطی که در آنها, نمودار دارای خط مماس افقی است در این جدول باشند. نمودار را نیز رسم کنید.
در نقاط مختلف روی نمودار بنویسید و دقت کنید تمام نقاطی که در آنها, نمودار دارای خط مماس افقی است در این جدول باشند. نمودار را نیز رسم کنید.
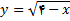
4.
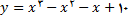
در تمرین های زیر, خط مماس و خط قائم را بر منحنی مفروض در نقطه مشخص شده را بدست اورید. نمودار منحنی و همچنین خطهای مماس و قائم را رسم کنید.
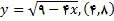
6.