معادلات دیفرانسیل / معادلات ديفرانسيل کامل
معادله مرتبه اول
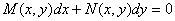 را كامل گوئيم هر گاه يك تابع دو متغيري (f(x,y وجود داشته باشد به طوري كه
را كامل گوئيم هر گاه يك تابع دو متغيري (f(x,y وجود داشته باشد به طوري كه
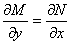
آنگاه
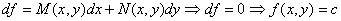
مثال:معادله ديفرانسيل زیر را حل كنيد.
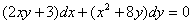
حل:
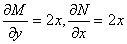
بنابر اين كامل است .
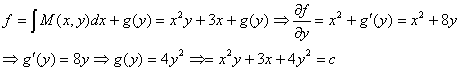
مثال:معادله ديفرانسيل زير را حل كنيد:
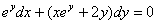
حل:
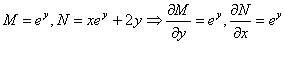
در نتيجه كامل است .
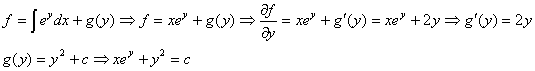
اگر معادله ديفرانسيل
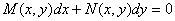 كامل نباشد گاهي مي توان يك تابع غير صفر
كامل نباشد گاهي مي توان يك تابع غير صفر
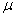 كه بستگي به x يا y يا هر دو متغير دارد يافت به طوري كه معادله
كه بستگي به x يا y يا هر دو متغير دارد يافت به طوري كه معادله
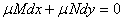 كامل باشد. در اين صورت
كامل باشد. در اين صورت 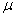 را يك عامل انتگرال ساز مي ناميم :
را يك عامل انتگرال ساز مي ناميم :
اگر
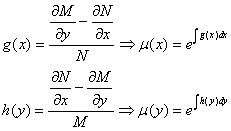
بدين شيوه عامل انتگرال ساز ساخته مي شود.
مثال:معادله ديفرانسيل 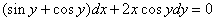 را حل كنيد.
را حل كنيد.
حل:
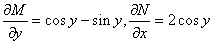
بنابر اين كامل نيست و در صورت وجود كامل انتگرال ساز را مي يابيم.
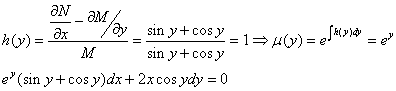
حال اين يك معادله ديفرانسيل كامل است.حل به عهده دانشجويان.
معادلات ديفرانسيل زير را حل كنيد:
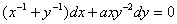
2.
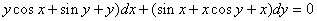
3.
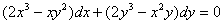
4.
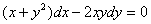
5.
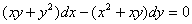
6.
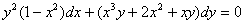
7.
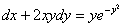
8.